Sous-sections
- Décomposition
- de A = E - F avec E inversible
- Algorithme
-

Dans la pratique, on utilise que 2 vecteurs 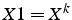 et
et 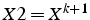
- Erreur
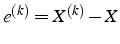
- par récursion
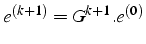
avec 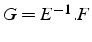 matrice de l'itération
matrice de l'itération
- La suite
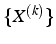 converge si
converge si
- théorème:
- la méthode itérative
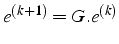 converge
si et seulement si le rayon spectral
converge
si et seulement si le rayon spectral 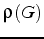 de la matrice G est
strictement inférieur à 1. Par définition
de la matrice G est
strictement inférieur à 1. Par définition
où 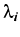 est la
est la 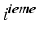 valeur propre de G
valeur propre de G
- remarque:
- théorème du point fixe
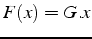 avec
avec 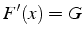 converge si
converge si
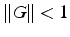
- décomposition de A :
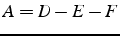
- D : diagonale de A
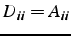 et
et 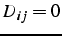 si
si 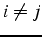
- E : matrice triangulaire inférieure
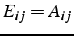 si
si 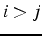 et
et 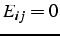 si
si 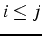
- F : matrice triangulaire supérieure
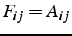 si
si 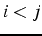 et
et 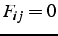 si
si 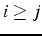
- itération
- de Jacobi
- théorème:
- Si A est une matrice à diagonale dominante, alors la
méthode de Jacobi converge
- définition:
- matrice à diagonale dominante
A est à diagonale dominante si
- Algorithme
-
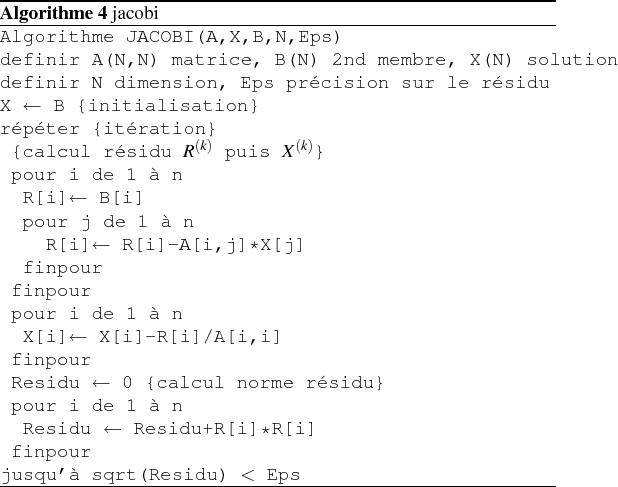
- utilisation de
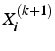 dès que calculé
dès que calculé
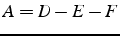 et
et 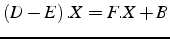
- itération de Gauss-Seidel
- matrice de l'itération
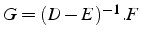
Attention on ne calcul pas 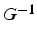 explicitement
explicitement
- théorème:
- Si A est une matrice à diagonale dominante, alors la
méthode de Gauss-Seidel converge
- Algorithme
-

paramêtre 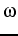 d'accélération de la convergence
d'accélération de la convergence
englishméthode GaussSeidel et SOR sous Maple
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2008-02-28

![]() et
et ![]()
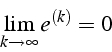
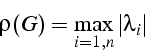
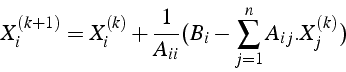
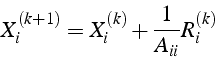
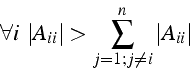

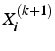 dès que calculé
dès que calculé
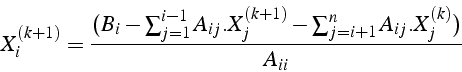

![]() d'accélération de la convergence
d'accélération de la convergence