Sous-sections
résolution itérative de 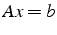 avec
avec 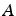 non singulière de dimension
non singulière de dimension
 .
.
- principe:
- soit
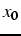 un vecteur initial, on veut calculer
une nouvelle estimation
un vecteur initial, on veut calculer
une nouvelle estimation 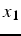 telle que le résidu
telle que le résidu
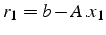 soit plus petit en norme que
soit plus petit en norme que
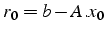 . Pour cela on choisit
une direction de descente
. Pour cela on choisit
une direction de descente 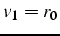 , et on impose que la projection
du nouveau résidu soit orthogonale à une direction
, et on impose que la projection
du nouveau résidu soit orthogonale à une direction 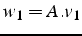 .
.
englishméthode du résidu minimum sous Maple
- Généralisation:
- on choisit un sous espace
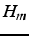 comme direction
de descente au lieu d'un vecteur.
comme direction
de descente au lieu d'un vecteur.
- Méthode de projection:
- soit
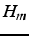 un sous espace de dimension
un sous espace de dimension
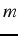 de
de
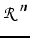 et
et 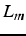 un second sous espace . On
cherche une correction
un second sous espace . On
cherche une correction 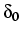 dans
dans 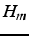 telle que le résidu
soit perpendiculaire à
telle que le résidu
soit perpendiculaire à 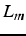 . On choisit
. On choisit 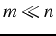 de façon à ce
que le système projeté soit de dimension petite (
de façon à ce
que le système projeté soit de dimension petite (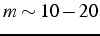 )
)
- espace de Krylov:
- on choisit un vecteur
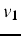 , et on construit
le sous-espace de Krylov
, et on construit
le sous-espace de Krylov
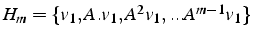 .
(remarque
.
(remarque
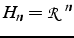 ). L'espace orthogonal
). L'espace orthogonal 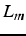

Pour améliorer la convergence, on préconditionne le système en effectuant
par exemple une factorisation incompléte de 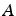 :
:
où 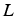 et
et 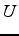 ont la même structure creuse que
ont la même structure creuse que 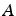 .
.
Le système préconditionné s'écrit:
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2008-02-28
![]() avec
avec ![]() non singulière de dimension
non singulière de dimension
![]() .
.

![]() :
:
![]() et
et ![]() ont la même structure creuse que
ont la même structure creuse que ![]() .
.