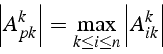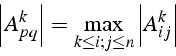Sous-sections
englishméthode d'élimination de Gauss pour un système 3*3 avec Maple
- transformation du système
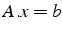
en un système triangulaire 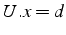
- résolution de
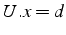
Pour 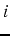 de
de 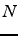 à
à 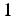
Algorithme
![\begin{algorithm}
% latex2html id marker 3108\caption{remont\'{e}
}
\par
\beg...
...i]$\leftarrow$(d{[}i]-somme)/U{[}i,i]
\par
finpour\end{list}\par
\end{algorithm}](img483.png)
- Détail
- de l'algorithme
- étape 1: élimination de
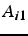 pour i de 2 à n
pour i de 2 à n
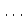
- étape k: élimination de
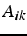 pour i de k+1 à n
pour i de k+1 à n
ligne i (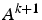 ) = ligne i (
) = ligne i (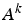 ) -
) -
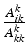 ligne k (
ligne k (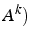
- Algorithme
-
![\begin{algorithm}
% latex2html id marker 3204\caption{factorisation
}
\par
\b...
...$B{[}i]-Coef{*}B{[}k]
\par
~~finpour
\par
finpour~\end{list}\par
\end{algorithm}](img503.png)
- coût
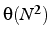 opérations
opérations
2 stratégies si 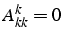
permutation de ligne à chaque étape k
remplace la ligne k par la ligne p telle que
- permutation
- ligne p colonne q pour amener en
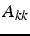 l'élément
l'élément
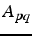 telle que
telle que
- remarque:
- si un pivot est nul apres pivotage partiel ou total,
alors la matrice
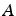 est singulière
est singulière
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2008-02-28
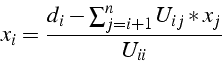
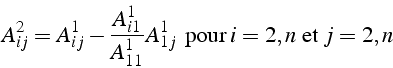
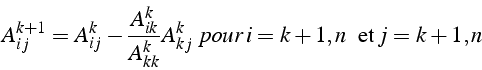
![\begin{algorithm}
% latex2html id marker 3204\caption{factorisation
}
\par
\b...
...$B{[}i]-Coef{*}B{[}k]
\par
~~finpour
\par
finpour~\end{list}\par
\end{algorithm}](img503.png)
![]()