suivant: 5.4 Précision monter: 5. Un second exemple précédent: 5.2 Résolution avec FEMLAB Table des matières
On reprend l'exemple précédent, en supposant que le cylindre tourne
à vitesse angulaire
![]() . On suppose
maintenant que le fluide est visqueux, pour pouvoir être entraîné
par le cylindre, mais reste irrotationnel. L'écoulement reste un écoulement
à potentiel, vérifiant une équation de Laplace:
. On suppose
maintenant que le fluide est visqueux, pour pouvoir être entraîné
par le cylindre, mais reste irrotationnel. L'écoulement reste un écoulement
à potentiel, vérifiant une équation de Laplace:
Les conditions aux limites sont telles que loin de l'obstacle la vitesse
est égale à ![]() . Pour la condition aux limites sur l'obstacle,
la condition physique est que la vitesse du fluide doit être égale
à la vitesse du cylindre
. Pour la condition aux limites sur l'obstacle,
la condition physique est que la vitesse du fluide doit être égale
à la vitesse du cylindre
![]() , Cependant, cette condition
aux limites n'est pas compatible avec les hypothèses de fluide irotationnel.
On impose donc une condition moins forte: l'égalité de l'intégrale
de la vitesse tangentielle sur le cylindre, et la condition d'imperméabilité,
soit
, Cependant, cette condition
aux limites n'est pas compatible avec les hypothèses de fluide irotationnel.
On impose donc une condition moins forte: l'égalité de l'intégrale
de la vitesse tangentielle sur le cylindre, et la condition d'imperméabilité,
soit
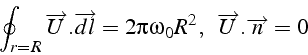
La première condition impose la circulation de vitesse ![]() autour
du cylindre:
autour
du cylindre:
qui peut s'interpréter comme la condition qu'en moyenne la vitesse
du fluide ![]() sur le cylindre est égale à la vitesse du
cylindre
sur le cylindre est égale à la vitesse du
cylindre ![]() .
.
La mise en rotation du fluide par le cylindre engendre autour du cylindre
une répartition de pression qui n'est plus symétrique par rapport
à ![]() . Cette répartition de pression crée une force de portance
sur le cylindre
. Cette répartition de pression crée une force de portance
sur le cylindre ![]() (suivant Oy):
(suivant Oy):
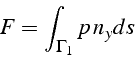
où ![]() est la composante suivant y de la normale
est la composante suivant y de la normale
![]() à la surface
à la surface ![]() . La théorie des écoulements potentiels montre
que cette force est proportionnelle à la circulation
. La théorie des écoulements potentiels montre
que cette force est proportionnelle à la circulation ![]()
Cette force de portance, perpendiculaire à la vitesse du fluide loin du cylindre, est appelée “effet Magnus” et explique les mouvements de lift des balles de tennis ou de golf.
Pour résoudre ce problème par éléments finis, on calcule une approximation
![]() de la fonction de courant
de la fonction de courant ![]() solution de:
solution de:
associée aux conditions aux limites:
La seconde conditions aux limites implique que le cylindre ![]() est une ligne de courant et la valeur
est une ligne de courant et la valeur ![]() imposée est
telle que l'on ait une circulation
imposée est
telle que l'on ait une circulation ![]() autour du cylindre.
autour du cylindre.
Les différentes étapes de la résolution sont:
description du model (version HTML)
execution du modele (version FEMLAB)
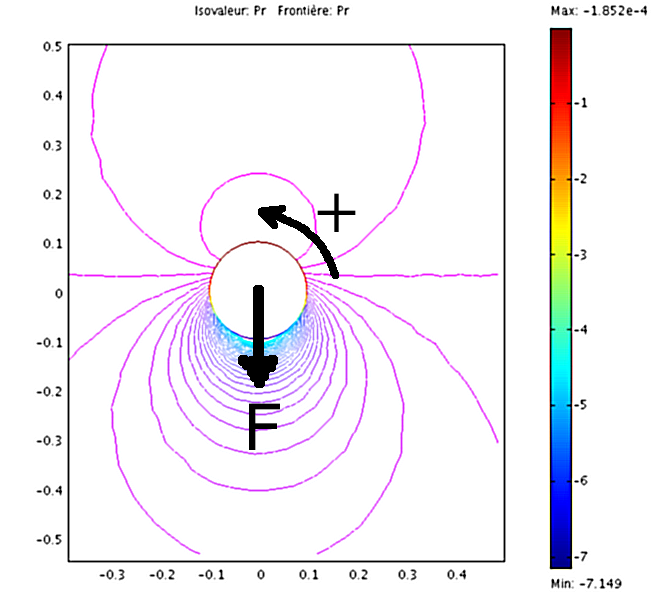
Pour analyser le résultat, on calcule tout d'abord le champ de pression en utilisant Bernoulli:
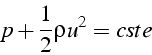
soit en fonction de ![]() (à une constante près)
(à une constante près)
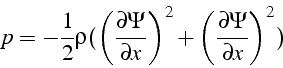
On en déduit la force de portance ![]()
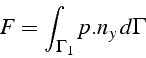
Avec FEMLAB, on obtiens pour ![]() ,
, ![]() ,
, ![]() et
et ![]() :
:
Le calcul de la circulation ![]() en fonction de
en fonction de ![]() s'écrit:
s'écrit:
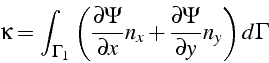
puisque
![]() .
.
Le calcul FEMLAB donne:
ce qui est en très bon accord avec la théorie (solution exacte 5.6),
qui pour une circulation positive, prédit une force de portance négative.
Compte tenu de la relation 5.5, on peut aussi en déduire
la vitesse de rotation ![]() du cylindre pour la valeur de
du cylindre pour la valeur de
![]() imposée:
imposée: