5.2 Résolution avec FEMLAB

FEMLAB est un programme qui permet de calculer l'approximation par éléments finis d'un problème physique. Les différentes étapes de la résolution sont:

1. choix du modèle physique (EDP) et choix du degré d'approximation (éléments $P^{2}$ par défaut).
2. création de la géométrie
3. maillage du domaine de calcul
4. définition des coefficients du modèle dans $\Omega$
5. définition des conditions aux limites sur la frontière $\Gamma=\partial\Omega$
6. résolution
7. analyse et tracé de la solution

Ces étapes sont décrites ci dessous:

description du model

description du model (version HTML)

5.2.1 Exécution du modèle FEMLAB

execution du modele (version FEMLAB)

5.2.2 Analyse du résultat

La solution analytique de ce problème s'écrit:

$$\Psi_{e}(x,y)=U_{0}r \sin\theta (1-\frac{R^{2}}{r^{2}})$$

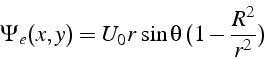
On peut alors calculer l'erreur entre cette solution exacte et la solution par élément finis, et on trouve

$$-9.3 10^{-3}\leq\Psi_{e}-\Psi^{h}\leq9.3 10^{-3} \mbox{avec} \left\vert\psi_{e}\right\vert\leq0.93$$

En analysant cette erreur, on peut s'apercevoir qu'une partie de l'erreur est due à la condition aux limites sur $\Gamma_{1}$, car avec les conditions aux limites imposées on a $\Psi^{h}\neq\Psi_{e}$ sur $\Gamma_{1}$. En imposant exactement sur $\Gamma_{1}$ $\Psi^{h}=\Psi_{e}$, on obtiens une erreur encore beaucoup plus faible:

$$-1.24 10^{-4}\leq\Psi_{e}-\Psi^{h}\leq9.5 10^{-5}$$