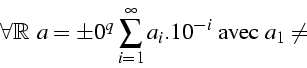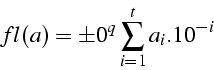Sous-sections
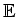
- sous-ensemble fini de
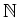
n=16 bits
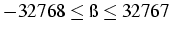
n=32 bits
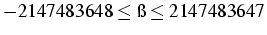
arithmétique exacte + - * /
- sous-ensemble fini de
 (
(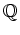 )
)
Réel 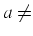 normalisé = mantisse+exposant
normalisé = mantisse+exposant
- représentation flottante
- (si
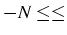 )
)
- simple précision 32 bits: t=7,
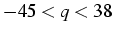
- double précision 64 bits: t=15,
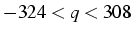
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2007-11-26