2.2 Introduction

précision d'un résultat numérique

1. erreurs de modélisation
2. erreurs de représentation sur ordinateur
3. erreurs de troncature (liés à la méthode)

Erreurs

erreur absolue $\Delta x=\left\vert x-x^{*}\right\vert$,
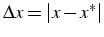erreur relative $Er(x)=\frac{\Delta x}{x}=\frac{\left\vert x-x^{*}\right\vert}{x}$

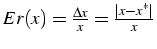
REMARQUE: en pratique on calcul une majoration 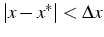$\left\vert x-x^{*}\right\vert<\Delta x$ et on note $x=x^{*}\pm\Delta x$.

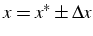Chiffres significatifs

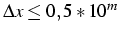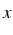si $\Delta x\le0,5*10^{m}$, alors le chiffre de $x$ correspondant à la 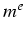$m^{e}$ puissance de 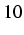$10$ est dit significatif (ainsi que tous ceux à gauche):

exemple: $\Delta x=\left\vert\Pi-\frac{22}{7}\right\vert=0,00126..<0,510^{-2}$
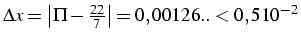
le chiffre des centièmes est significatifs et on a 3 chiffres significatifs.