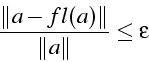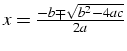Sous-sections
![\begin{algorithm}
% latex2html id marker 189
[H]
\par
\caption{précision machine...
...recis $\leftarrow\epsilon$ \{ precision machine \}\end{list}\par
\end{algorithm}](img43.png)
-
Pour une représentation avec t chiffres:
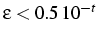
- erreur sur les opérations
- opérations arithmétiques inexactes + - * /
- non associativité de l'addition et soustraction
- formule exacte
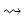 résultats numériques faux
résultats numériques faux
- exemple
-
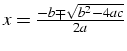
calcul simple précision avec
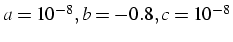
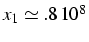 et
et
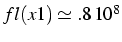
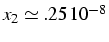 et
et
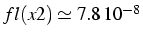
- formules instables = soustraction de quantités voisines
- accumulation des erreurs élémentaires
 erreur sur des sommes ou produits non négligeables
erreur sur des sommes ou produits non négligeables
- exemple
- calcul de
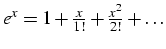 pour
pour 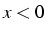 série alternée sur un ordinateur avec t=14
série alternée sur un ordinateur avec t=14
| x |
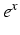 |
Somme
-10 |
- Conditionnement
- sensibilité du résultat à une petite variation
des données.
Problème mal conditionné=grande sensibilité vis à vis des données.
- Stabilité
- sensibilité de l'algorithme vis a vis des erreurs numériques
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2007-11-26