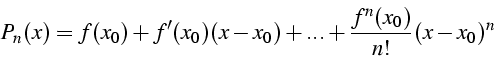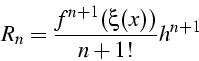2.5 Erreurs de troncature

2.5.1 Développement de Taylor

Polynôme

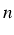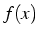Taylor de degré $n$ de $f(x)$ autour de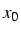 $x_{0}$

$$P_{n}(x)=f(x_{0})+f'(x_{0})(x-x_{0})+...+\frac{f^{n}(x_{0})}{n!}(x-x_{0})^{n}$$

théorème:

Erreur de troncature $R_{n}$

$$f(x)=P_{n}(x)+R_{n}\mbox{ et }h=x-x_{0}$$

$$R_{n}=\frac{f^{n+1}(\xi(x))}{n+1!}h^{n+1}$$

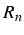
Ordre $O(h^{n})$:

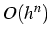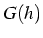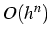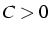La fonction $G(h)$ est en $O(h^{n})$ s'il existe une constante $C>0$ telle que $\left\vert G(h)\right\vert<Ch^{n}$

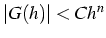
Approximation d'ordre n:

si l'erreur est en 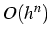$O(h^{n})$, alors l' approximation est d'ordre n