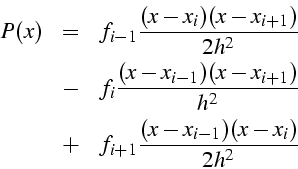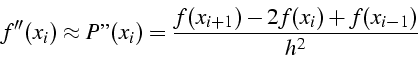suivant: 9.3 Principe d'intégration numérique monter: 9. Equations différentielles précédent: 9.1 Introduction Table des matières
f(x) définie par ses valeurs en n+1 points ![]()
Estimation de la dérivée ![]()
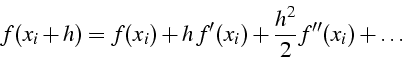
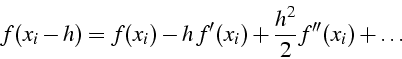
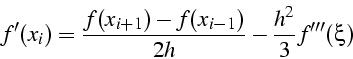
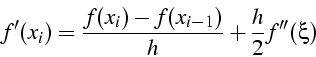
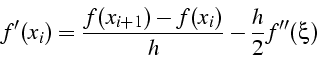
formules équivalentes :
polynôme d'ordre 2 ![]() formule centrée ordre 2
formule centrée ordre 2
polynôme d'ordre 1 ![]() formule décentrée ordre 1
formule décentrée ordre 1
D.L de ![]() et
et ![]() au voisinage de
au voisinage de ![]() :
:
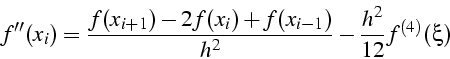
Polynôme d'interpolation P(x) de degré 2