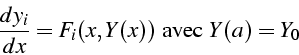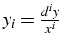suivant: 9.2 Formules de dérivation monter: 9. Equations différentielles précédent: 9. Equations différentielles Table des matières
Soit ![]() une fonction de
une fonction de
![]() sur
sur
![]() , on cherche la solution
, on cherche la solution ![]() sur
sur ![]() de l'équation
différentielle du premier ordre y(x)
de l'équation
différentielle du premier ordre y(x)
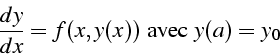
C'est un problème aux valeurs initiales ou ``Problème de Cauchy''
alors le problème de Cauchy admet une solution unique sur [a,b]
![]()