8.3 Méthodes composites

décomposition de [a,b] en n sous-intervalles:

Formule de Newton-Côtes sur chaque intervalle

8.3.1 Méthode des trapèzes

n intervalles, $h=\frac{b-a}{n}$, (n+1) pts $x_{i}=a+i*h$

$$\int_{a}^{b}{f(x) dx}\simeq h\left(\frac{f(a)+f(b)}{2}+\sum_{i=1}^{n-1}{f(a+ih)}\right)$$

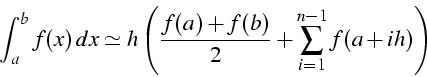
estimation de l'erreur Err(n) avec $n=\frac{b-a}{h}$ (méthode d'ordre 2)

$$Err(n)\leq\frac{(b-a)^{3}}{12n^{2}}\max_{x\in[a,b]}{\left\vert f''(x)\right\vert}$$

8.3.2 Méthode de SIMPSON

n intervalles, $2h=\frac{b-a}{n}$, (2n+1) pts $x_{i}=a+i*h$

$$\begin{eqnarray*} \int_{a}^{b}{f(x) dx} & \simeq & \frac{h}{3}\left(f(a)+f(b)+... ...+2ih)}\right.\\ & & \left.+4\sum_{i=1}^{n}{f(a+(2i-1)h)}\right)\end{eqnarray*}$$

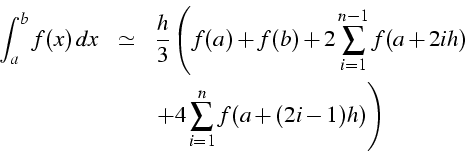
estimation de l'erreur Err(n) avec $n=\frac{b-a}{2h}$ (méthode d'ordre 4)

$$Err(n)\leq\frac{(b-a)^{5}}{180(2n)^{4}}\max_{x\in[a,b]}{\left\vert f^{(4)}(x)\right\vert}$$