Sous-sections
On approche f(x) par le polynôme d'interpolation P(x).
Problème du choix des abscisses 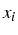
- subdivision régulière de
![$[a,b]$](img89.png)
- choisir les
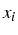 ``au mieux''
``au mieux''
- théorème:
- Une formule de quadrature à (n+1) points est exacte
pour tous les polynômes de degré au plus n si et seulement si elle
est du type interpolation à (n+1) points . (i.e. P(x) est le polynôme
d'interpolation de f(x))
- Application:
- calcul des coefficients
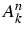 par "la
méthode des coefficients indéterminés".
par "la
méthode des coefficients indéterminés".
- exemple:
- calcul de
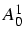 et
et 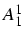 t.q.
t.q.
avec f(x) = 1 et x, on obtient un système 2*2, d'où
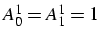
subdivision régulière de [a,b]
- formule du trapèze (n=1)
- formule de Simpson (n=2)
majoration de l'erreur R(h) avec h=b-a:
D.L. de R(h) au voisinage de h=0
majoration de l'erreur R(h) avec
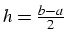 et
et
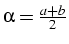 :
:
D.L. de R(h) au voisinage de h=0
- théorème:
- Pour un nombre de points (n+1) dans les formules de
Newton-Côtes, si n est pair l'erreur est en
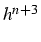 , par contre
si n est impair l'erreur est en
, par contre
si n est impair l'erreur est en 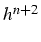
- remarque:
- Si n impair la précision est n, si n pair la précision
est n+1. Attention Formules instables !!.
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2007-11-26
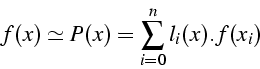
![]()
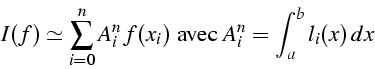
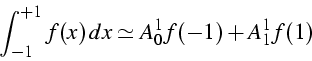
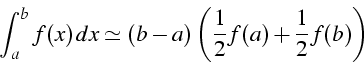
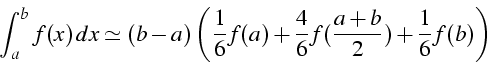
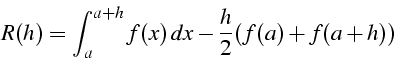
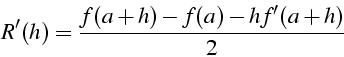
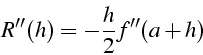
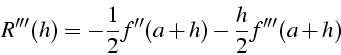
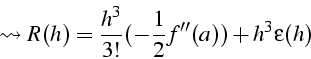
![\begin{displaymath}
\left\vert R(f)\right\vert\leq\frac{h^{3}}{12}\max_{x\in[a,b]}\left\vert f''(x)\right\vert\end{displaymath}](img457.png)
![]() et
et
![]() :
:
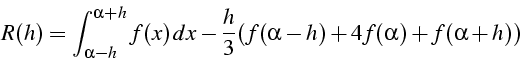
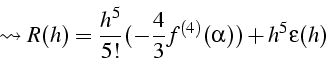
![\begin{displaymath}
\left\vert R(f)\right\vert\leq\frac{h^{5}}{90}\max_{x\in[a,b]}\left\vert f^{(4)}(x)\right\vert\end{displaymath}](img462.png)