suivant: 9. Equations différentielles monter: 8. Intégration numérique précédent: 8.3 Méthodes composites Table des matières
choix des points ![]() "au mieux", t.q. la formule
de quadrature
"au mieux", t.q. la formule
de quadrature
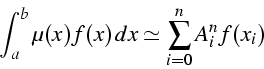
soit exacte pour les polynômes de degrés de plus élevés.
Pour le cas ![]() les valeurs des coefficients sont données
dans la table ci dessous
les valeurs des coefficients sont données
dans la table ci dessous
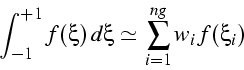
| ordre | formule | poids | position |
paramètres
1 |