suivant: 6.4 Interpolation de Chebycheff monter: 6. Interpolation polynomiale précédent: 6.2 Interpolation de Lagrange Table des matières
soit f(x) fonction de classe ![]()
soient n+1 points
![]()
![\begin{displaymath}
f(x)-p(x)=\frac{\prod_{i=0}^{n}(x-x_{i})}{(n+1)!}f^{n+1}(\xi)\mbox{ avec }\xi\in[a,b]\end{displaymath}](img356.png)
W(t) s'annule en n+2 points : ![]() (i=0,n) et x
(i=0,n) et x
donc W'(t) s'annule en n+1 points (théorème de Rolle)
donc ![]() s'annule une fois en
s'annule une fois en ![]()
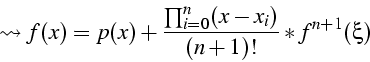
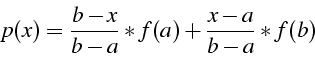
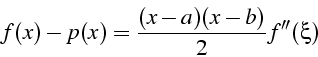
![\begin{displaymath}
\left\vert f(x)-p(x)\right\vert\leq\frac{\left\vert\prod_{i=...
...t}{(n+1)!}*\max_{\xi\in[a,b]}\left\vert f^{n+1}(\xi)\right\vert\end{displaymath}](img367.png)