6.4 Interpolation de Chebycheff

6.4.1 introduction

Détermination des points d'interpolations $x_{i}$ de façon à minimiser l'erreur d'interpolation indépendamment de f(x).

Ces points sont les racines d'un polynôme T(x) de $E^{n}$

$$T(x)=\prod_{i=0}^{n}(x-x_{i})$$

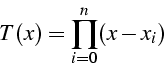
$E^{n}$ ensemble des polynômes de degré n sur [-1,1] avec un coefficient de $x^{n}$ égal à 1:

$$?\exists T\in E^{n}\mbox{ : }\max\left\vert T(x)\right\vert\leq\max\left\vert p(x)\right\vert \forall p(x)\in E^{n}$$

6.4.2 construction

formule de Moivre:

$(\cos\theta+\imath\sin\theta)^{n}=\cos(n\theta)+\imath\sin(n\theta)$

en posant $x=cos\theta$ et $\sqrt{1-x^{2}}=sin\theta$

$$cos(n\theta)=x^{n}-C_{n}^{2}x^{n-2}(1-x^{2})+C_{n}^{4}x^{n-4}(1-x^{2})^{2}+\ldots$$

$\leadsto$polynôme de degré n en x :  $T_{n}(x)=\cos(n\theta)$

$T_{n}(x)$ polynôme de Chebycheff de degré n

$T_{0}(x)=1$; $T_{1}(x)=x$; $T_{2}(x)=2x^{2}-1$;

$T_{3}(x)=4x^{3}-3x$

6.4.3 propriétés

relation 1

 

$$T_{n+1}(x)=2x*T_{n}(x)-T_{n-1}(x)$$

démonstration:

calcul $cos(n\theta+\theta)$ et $cos(n\theta-\theta)$

relation 2:

Le coefficient du terme en $x^{n}$ de $T_{n}(x)$ est $2^{n-1}$

démonstration:

par récurrence

relation 3: Le

polynôme $Tn(x)$ possède n zéros
$x_{k}=cos(\frac{(2k-1)\pi}{2n})$ (k=1,n)
atteint son extremum sur [-1,1] en n+1 points
$x'_{k}=cos(\frac{k\pi}{n})$ (k=0,n)
avec $T(x'_{k})=\pm1$

démonstration:

vérification directe
$T_{n}(x)=\cos(n\arccos(x))$ et
$T'_{n}(x)=\sin(n\arccos(x))*\frac{n}{\sqrt{(}1-x^{2})}$

6.4.4 polynôme normalisé

théorème:

Le polynôme $\bar{T}(x)=\frac{1}{2^{n-1}}T(x)$ vérifie :

$$Sup_{-1\leq x\leq1}\left\vert T(x)\right\vert\leq Sup_{-1\leq x\leq1}\left\vert p(x)\right\vert \forall p(x)\in E^{n}$$

démonstration:

par l'absurde avec un autre polynôme p(x)
$T_{n}(x)$ atteint sa valeur maximale n+1 fois
$r(x)=T_{n}(x)-p(x)$ de degré n-1 s'annule n fois