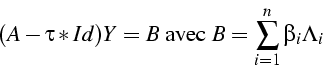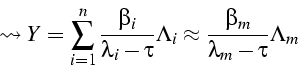suivant: 5.9 Algorithme QR monter: 5. Méthodes itératives de précédent: 5.7 Problème aux valeurs Table des matières
Détermination de la plus grande des v.p.
![]()
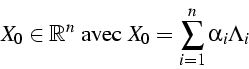
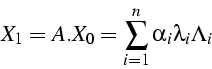
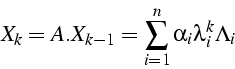
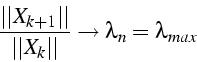

Détermination d'une valeur propre ![]()
et du vecteur propre associé ![]()