suivant: 3.3 Équation de transport monter: 3. Étude de schémas précédent: 3.1 Introduction Table des matières
On veut calculer la température
![]() dans un barreau de longueur
dans un barreau de longueur
![]() , de section
, de section
![]() , de masse volumique
, de masse volumique
![]() dont l'extrémité
gauche est maintenue à température constante (i.e
dont l'extrémité
gauche est maintenue à température constante (i.e
![]() ),
et l'extrémité droite reçoit un flux de chaleur
),
et l'extrémité droite reçoit un flux de chaleur
![]() . En plus
de la conduction dans le solide (le flux de chaleur par conduction
dans une section s'écrit
. En plus
de la conduction dans le solide (le flux de chaleur par conduction
dans une section s'écrit
![]() ),
le barreau échange de la chaleur par convection avec l'air ambiant
à la température
),
le barreau échange de la chaleur par convection avec l'air ambiant
à la température
![]() sur toute sa longueur. En notant
sur toute sa longueur. En notant
![]() le coefficient d'échange par convection par unité de surface, le flux
de chaleur par convection s'écrit pour un élément de longueur
le coefficient d'échange par convection par unité de surface, le flux
de chaleur par convection s'écrit pour un élément de longueur
![]() :
:
![]() (où
(où
![]() est le périmètre
de la section du barreau).
est le périmètre
de la section du barreau).
L'équation de conservation de l'énergie s'écrit:
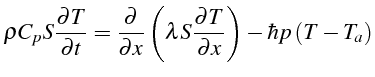
En notant
![]() , la conductivité du
matériau,
, la conductivité du
matériau,
![]() ,
,
![]() et
et
![]() la température relative, le problème modèle s'écrit:
la température relative, le problème modèle s'écrit:
Trouver
![]() solution du système (3.1):
solution du système (3.1):
La fonction
![]() correspond à la condition initiale du problème.
correspond à la condition initiale du problème.
Nous allons utiliser le programme Maple 3.2.2 pour déterminer
la solution générale
![]() de l'équation (3.1). Pour
cela nous décomposons la solution
de l'équation (3.1). Pour
cela nous décomposons la solution
![]() (lignes 4 et 5) en la
somme de la solution stationnaire
(lignes 4 et 5) en la
somme de la solution stationnaire
![]() et de la solution transitoire
homogène
et de la solution transitoire
homogène
![]() .
.
La solution stationnaire
![]() est solution du problème suivant
(lignes 8 à 9) (en notant
est solution du problème suivant
(lignes 8 à 9) (en notant
![]() ):
):
que l'on résout directement avec la fonction Maple dsolve
(ligne 10). Le résultat est simplifié en introduisant les fonctions
hyperboliques
![]() et
et
![]() (ligne 11 à 15):
(ligne 11 à 15):
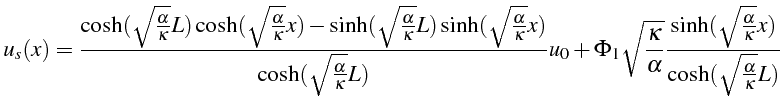
On vérifie (ligne 21) que cette solution tend vers la solution linéaire
de diffusion pure lorsque
![]() :
:
# Solution analytique de l'équation de la chaleur avec source
> restart:with(plots):
# Equation et conditions aux limites
> diff(u(t,x),t)-K*diff(u(t,x),x$2)+alpha*u(t,x)=0;eq:=%:
> u(t,0)=u0; diff(u(t,x),x)=Phi[1];
# Equation stationnaire
> beta=sqrt(alpha/K);
> -diff(U(x),x$2)+beta^2*U(x)=0; eqs:=%:
> U(0)=u0,D(U)(L)=Phi[1];CL:=%:
> dsolve({eqs,CL},U(x));rel1:=%:
> simplify(subs(exp(beta*L)=cosh(beta*L)+sinh(beta*L),
> exp(-beta*L)=cosh(beta*L)-sinh(beta*L),
> exp(beta*x)=cosh(beta*x)+sinh(beta*x),
> exp(-beta*x)=cosh(beta*x)-sinh(beta*x),
> rel1));collect(%,[beta,u0]);
# solution stationnaire
> subs(beta=sqrt(alpha/K),%);sols:=%: Us:=rhs(%):
> simplify(subs(U(x)=Us,subs(beta=sqrt(alpha/K),eqs)));
> subs(K=1,alpha=1,L=1,u0=1,Phi[1]=0,Us);
> plot(%,x=0..1);
# Cas particulier alpha=0
> limit(sols,alpha=0);
# Solution instationnaire equation homogene
> diff(u(t,x),t)-K*diff(u(t,x),x$2)+alpha*u(t,x)=0;eqi:=%:
> u(t,0)=0; diff(u(t,x),x)=0;
# Separation de variables
> u(t,x)=A(t)*B(x);
> expand(subs(u(t,x)=A(t)*B(x),eqi/(A(t)*B(x))));rel2:=%:
> op(lhs(rel2))[1]+op(lhs(rel2))[3]=-op(lhs(rel2))[2]; %/K;eq1:=%:
# Les 2 membres sont constants et <0 = -omega^2
> rhs(eq1)=-omega^2; eq2:=%:
> B(0)=0,D(B)(L)=0;CL:=%:
> dsolve({eq2,B(0)=0},B(x));
> omega=(2*k+1)*Pi/2/L;rel5:=%:
> lhs(eq1)=-omega^2;%*K;
> dsolve(%,A(t));
# Solution elementaire
> sin(omega*x)*exp(-(alpha+omega^2*K)*t);
> subs(rel5,%);rel6:=%:
# Solution générale du problème transitoire
> sum(C[k]*rel6,k=0..N); Ug:=%:
# Solution exacte du probleme initiale
> Ue:=Us+Ug;
L'allure de cette solution est donnée sur la figure (3.2) (ligne 19).
La solution transitoire
![]() est solution du problème homogène
suivant (lignes 23 et 24):
est solution du problème homogène
suivant (lignes 23 et 24):
dont on cherche la solution par une méthode de séparation de variables.
On pose
![]() (ligne 26) et l'équation 3.3
devient (lignes 27 à 29)
(ligne 26) et l'équation 3.3
devient (lignes 27 à 29)
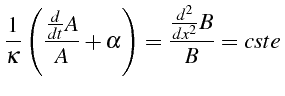 avec
avec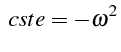
Chacun des membres de l'égalité doit être constant et négatif (on
montre que si la constante est positive, alors
![]() ).
).
La solution
![]() est obtenue directement avec la fonction dsolve
(lignes 31 à 33) en utilisant la condition aux limites en
est obtenue directement avec la fonction dsolve
(lignes 31 à 33) en utilisant la condition aux limites en
![]() .
L'imposition de la condition en
.
L'imposition de la condition en
![]() fixe les valeurs possibles
de
fixe les valeurs possibles
de
![]() (ligne 34):
(ligne 34):
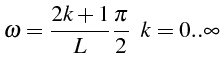
La solution
![]() est aussi calculée avec dsolve (lignes
35 à 36):
est aussi calculée avec dsolve (lignes
35 à 36):
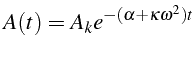
La solution générale est une combinaison linéaire de ces solutions élémentaires (ligne 41):
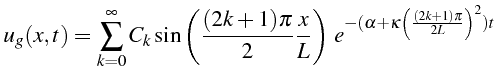
d'où la solution générale
![]() du problème (3.1)
du problème (3.1)
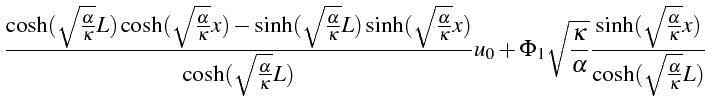 |
|||
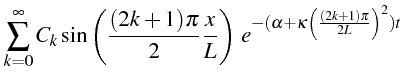 |
Les coefficients
![]() sont déterminées de façon à vérifier la condition
initiale
sont déterminées de façon à vérifier la condition
initiale
![]() . Ce sont les coefficients de Fourier de
. Ce sont les coefficients de Fourier de
![]() .
.
Dans la pratique, nous calculerons une solution tronquée sur
![]() modes, i.e. avec une somme finie
modes, i.e. avec une somme finie
![]() au lieu de la somme
à priori infinie
au lieu de la somme
à priori infinie
![]() dans l'expression précédente.
Déterminons ces coefficients dans les deux cas particuliers suivants.
dans l'expression précédente.
Déterminons ces coefficients dans les deux cas particuliers suivants.
Pour une condition initiale correspondant à la perturbation
![]() par rapport à la solution stationnaire, la solution pour
par rapport à la solution stationnaire, la solution pour
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() est calculée à la ligne
45 et tracé à la ligne 46 .
est calculée à la ligne
45 et tracé à la ligne 46 .
En notant
![]() le temps caractéristique
de diffusion, on a tracé sur la figure (3.3a) l'évolution
temporelle de cette solution
le temps caractéristique
de diffusion, on a tracé sur la figure (3.3a) l'évolution
temporelle de cette solution
# cas particulier avec 1 seul mode > U0:=unapply(eval(subs(N=0,Phi[1]=0,u0=1,Ue)),t,x); > Ui:=U0(0,x); # cas d'une condition initiale constante U=1 > U1:=unapply(eval(subs(Phi[1]=0,u0=1,L=1,sqrt(alpha/K)=beta,Ue)),t,x); > U1(0,x)=1; Ui:=subs(Phi[1]=0,u0=1,L=1,sqrt(alpha/K)=beta,Us); # calcul des coefficients de Fourier Ck > Int(Ui*sin((2*k+1)*Pi/2*x),x=0..1)+C[k]*Int(sin((2*k+1)*Pi/2*x)^2,x=0. > .1)=Int(sin((2*k+1)*Pi/2*x),x=0..1); # Calcul des differents termes de cette expression > k:='k':int(Ui*sin((2*k+1)*Pi/2*x),x=0..1); > simplify(subs(sin(k*Pi)=0,%));rel8:=%: > simplify(numer(rel8)/expand(denom(rel8)));rel9:=%: > 2*(2*k+1)*Pi/(4*beta^2+Pi^2*(2*k+1)^2);rel10:=%: > simplify(rel9-rel10); > int(sin((2*k+1)*Pi/2*x),x=0..1);simplify(subs(sin(k*Pi)=0,%)); > rel11:=%: > int(sin((2*k+1)*Pi/2*x)^2,x=0..1);simplify(subs(sin(k*Pi)=0,%)); > rel12:=%: > rel12*C[k]=rel11-rel10; # D'ou l'expression des Ck et d la solution > C[k]=(rel11-rel10)/rel12; rel13:=rhs(%): > U2:=unapply(subs(C[k]=rel13,beta=1,K=1,N=20,U1(t,x)),t,x);
Pour déterminer la solution, on calcule les coefficients
![]() en multipliant la condition initiale
en multipliant la condition initiale
![]() par
par
![]() et en intégrant de
et en intégrant de
![]() à
à
![]() (lignes 51 à 53). On laisse Maple faire les intégrations (lignes
55 à 64) en simplifiant les expressions et on obtiens les coefficients
(lignes 51 à 53). On laisse Maple faire les intégrations (lignes
55 à 64) en simplifiant les expressions et on obtiens les coefficients
![]() (lignes 67):
(lignes 67):
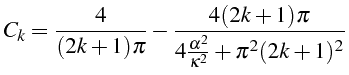
On trace l'allure de la solution calculée avec
![]() modes sur la
figure (3.3b) pour
modes sur la
figure (3.3b) pour
![]() variant de
0
à
variant de
0
à
![]() .
.
Le
![]() -schéma est obtenue par combinaison linéaire d'un schéma
explicite (
-schéma est obtenue par combinaison linéaire d'un schéma
explicite (
![]() ) et d'un schéma implicite (
) et d'un schéma implicite (
![]() ) . Il
s'écrit pour l'équation (3.1):
) . Il
s'écrit pour l'équation (3.1):
Le
![]() -schéma est un schéma implicite (sauf pour
-schéma est un schéma implicite (sauf pour
![]() )
qui couple les valeurs inconnues
)
qui couple les valeurs inconnues
![]() à l'étape
à l'étape
![]() aux valeurs connues
aux valeurs connues
![]() à l'étape
à l'étape
![]() comme indiqué sur le diagramme (3.4).
comme indiqué sur le diagramme (3.4).
Nous allons tout d'abord étudier les propriétés de ce schéma en utilisant Maple.
Dans le programme Maple (3.2.4), on effectue l'étude de la
stabilité du
![]() -schéma (3.5). Pour cela on définit
l'équation exacte (ligne 3), et l'équation discrétisée (ligne 6),
que l'on stocke dans les variables eq et eqh. La
perturbation
-schéma (3.5). Pour cela on définit
l'équation exacte (ligne 3), et l'équation discrétisée (ligne 6),
que l'on stocke dans les variables eq et eqh. La
perturbation
![]() est définie à la ligne 10, comme le mode
de Fourier
est définie à la ligne 10, comme le mode
de Fourier
![]() . L'équation étant homogène,
l'équation sur la perturbation est l'équation discrète eqh
dans laquelle on remplace la solution numérique
. L'équation étant homogène,
l'équation sur la perturbation est l'équation discrète eqh
dans laquelle on remplace la solution numérique
![]() par la perturbation
par la perturbation
![]() (ligne 11). On simplifie cette équation (ligne 12),
et l'on en déduit le facteur d'amplification
(ligne 11). On simplifie cette équation (ligne 12),
et l'on en déduit le facteur d'amplification
![]() .
Pour simplifier l'expression de
.
Pour simplifier l'expression de
![]() , on pose
, on pose
![]() et on introduit les 2 paramètres
et on introduit les 2 paramètres
![]() et
et
![]() suivants:
suivants:
On obtiens ainsi le facteur d'amplification
![]() (ligne 17):
(ligne 17):
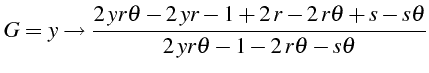
La condition de stabilité impose:
# Etude du theta-schema pour l'équation de la chaleur
> restart:
> eq:=diff(U(t,x),t)-kappa*diff(U(t,x),x$2)+alpha*U(t,x)=0:eq;
# Discretisation DF (theta schema)
> delta2:=(f,n)->(f[n,i+1]-2*f[n,i]+f[n,i-1])/dx^2;
> eqh:=(U[n+1,i]-U[n,i])/dt-kappa*(theta*delta2(U,n+1)+(1-theta)*
delta2(U,n))+theta*alpha*U[n+1,i]+(1-theta)*alpha*U[n,i]=0:
> eqh;
# Etude de la stabilite: introduction d'une perturbation
> Up:=(n,i)->Psi[n]*exp(I*omega*i*dx);
> subs(U[n,i]=Up(n,i),U[n,i+1]=Up(n,i+1),U[n,i-1]=Up(n,i-1),
U[n+1,i]=Up(n+1,i),U[n+1,i+1]=Up(n+1,i+1),
U[n+1,i-1]=Up(n+1,i-1),eqh);
> eqhp:=%:
> expand(simplify((eqhp)*dt*exp(-I*omega*i*dx)));rel1:=%:
> G:=solve(simplify(subs(Psi[n+1]=G*Psi[n],rel1/Psi[n])),G);
> G:=simplify(subs(cos(omega*dx)=y,alpha=s/dt,kappa=r*dx^2/dt,G));
# Schema explicite theta=0
> G0:=unapply(subs(theta=0,G),y);
> plot(subs(r=1/2,s=1/2,G0(y)),y=-1..1);
> G0(1)>-1;
> G0(-1)>-1;
> s<2;2>s+4*r;cdt1:=%:
> subs(r=kappa*dt/dx^2,s=alpha*dt,cdt1);
# Condition de stabilité pour le schema explicite
> (alpha+4*kappa/dx^2)*dt<2;
# Schema implicite theta=1
> G1:=unapply(subs(theta=1,G),y);
> plot(subs(r=1,s=1,G1(y)),y=-1..1);
> simplify(G1(-1));simplify(G1(1));
# Schema inconditionellement stable
# Schema C.N. theta=0.5
> G2:=unapply(subs(theta=1/2,G),y);
> plot(subs(r=1,s=1,G2(y)),y=-1..1);
> simplify(G2(-1));simplify(G2(1));
> G2(1)>-1;numer(G2(1))>-denom(G2(1));
> G2(-1)>-1; numer(G2(-1))>-denom(G2(-1));
# Schema inconditionellement stable
Pour simplifier, nous ferrons l'analyse pour les 3 valeurs suivantes
de
![]() :
:
![]() .
.
Dans ce cas, l'expression de
![]() est donnée à la ligne 19
est donnée à la ligne 19
C'est une fonction croissante de
![]() , inférieure à 1 pour
, inférieure à 1 pour
![]() .
La condition
.
La condition
![]() implique donc
implique donc
![]() , qui
s'écrit (ligne 23):
, qui
s'écrit (ligne 23):
En exprimant
![]() et
et
![]() en fonction de
en fonction de
![]() et
et
![]() , on obtiens
la condition de stabilité (ligne 24):
, on obtiens
la condition de stabilité (ligne 24):
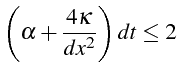
Cette condition impose une valeur maximum du pas en temps
![]() pour
un maillage en espace donnée (i.e. pour
pour
un maillage en espace donnée (i.e. pour
![]() fixé):
fixé):
Pour
![]() , on retrouve la condition de stabilité classique
, on retrouve la condition de stabilité classique
![]() . Pour
. Pour
![]() , on a une
équation différentielle en temps et on retrouve la condition de stabilité
de la méthode d'intégration d'Euler
, on a une
équation différentielle en temps et on retrouve la condition de stabilité
de la méthode d'intégration d'Euler
![]() .
.
Le schéma explicite est donc conditionnellement stable avec une condition de stabilité donnée par la relation (3.7).
Pour
![]() , l'expression de
, l'expression de
![]() est donnée à la ligne 28
est donnée à la ligne 28
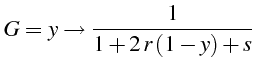
C'est une fonction croissante de
![]() , qui est comprise entre 0 et
1 pour
, qui est comprise entre 0 et
1 pour
![]() . On le vérifie facilement en traçant la fonction
. On le vérifie facilement en traçant la fonction
![]() (ligne 29) et en calculant
(ligne 29) et en calculant
![]() et
et
![]() (ligne 30) .
(ligne 30) .
Le schéma implicite est donc inconditionnellement stable.
Pour
![]() , l'expression de
, l'expression de
![]() est donnée à la ligne
33
est donnée à la ligne
33
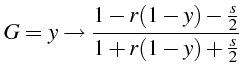
C'est une fonction croissante de
![]() , qui est comprise entre -1 et
1 pour
, qui est comprise entre -1 et
1 pour
![]() . On le vérifie facilement en traçant la fonction
. On le vérifie facilement en traçant la fonction
![]() (ligne 34) et en calculant
(ligne 34) et en calculant
![]() et
et
![]() (lignes 35 à 37)
.
(lignes 35 à 37)
.
Le schéma de Crank Nicholson est donc inconditionnellement stable.
Pour étudier la consistance du
![]() -schéma, nous utiliserons
le programme Maple (3.2.5). Pour cela on définit l'équation
exacte (ligne 3), et l'équation discrétisée (ligne 6), que l'on stocke
dans les variables eq et eqh.
-schéma, nous utiliserons
le programme Maple (3.2.5). Pour cela on définit l'équation
exacte (ligne 3), et l'équation discrétisée (ligne 6), que l'on stocke
dans les variables eq et eqh.
# Etude du theta-schema pour l'équation de la chaleur > restart: > eq:=diff(U(t,x),t)-kappa*diff(U(t,x),x$2)+alpha*U(t,x)=0:eq; # Discretisation DF (theta schema) > delta2:=(f,n)->(f[n,i+1]-2*f[n,i]+f[n,i-1])/dx^2; > eqh:=(U[n+1,i]-U[n,i])/dt-kappa*(theta*delta2(U,n+1)+(1-theta)* delta2(U,n))+theta*alpha*U[n+1,i]+(1-theta)*alpha*U[n,i]=0: > eqh; # Etude de la consistence # calcul de l'erreur de troncature > Uex:=(p,q)->U(t+(p-n)*dt,x+(q-i)*dx); > subs(U[n,i]=Uex(n,i),U[n,i+1]=Uex(n,i+1),U[n,i-1]=Uex(n,i-1), U[n+1,i]=Uex(n+1,i),U[n+1,i+1]=Uex(n+1,i+1), U[n+1,i-1]=Uex(n+1,i-1),lhs(eqh)); > rel3:=%: > expand(simplify(rel3-lhs(eq)));rel4:=%: # Developpement en serie de Taylor > U(t+dt,x)=convert(mtaylor(U(t+dt,x),[dt],4),diff);S1:=%: > U(t+dt,x+dx)=convert(mtaylor(U(t+dt,x+dx),[dt,dx],4),diff); S2:=%: > U(t+dt,x-dx)=convert(mtaylor(U(t+dt,x-dx),[dt,dx],4),diff); S3:=%: > U(t,x+dx)=convert(mtaylor(U(t,x+dx),[dx],5),diff);S4:=%: > U(t,x-dx)=convert(mtaylor(U(t,x-dx),[dx],5),diff);S5:=%: > simplify(subs(S1,S2,S3,S4,S5,rel4)): > ErrT:=collect(%,dt); # Calcul du coefficient du terme en dt > coeff(ErrT,dt);c1:=%: > diff(eq,t); > factor(simplify(c1+theta*lhs(%))); # Donc schema en O(dt,dx^2) si theta#1/2 et O(dt^2,dx^2) sinon
On remplace ensuite dans l'équation discrétisée eqh la solution
numérique
![]() par la solution exacte
par la solution exacte
![]() définie
à la ligne 11. La fonction
définie
à la ligne 11. La fonction
![]() est définie de sorte à faire
apparaître les solutions à
est définie de sorte à faire
apparaître les solutions à
![]() ,
,
![]() ou
ou
![]() . Cette substitution
est faite à la ligne 12 et le résultat est stocké dans la variable
rel3. On calcul l'erreur de troncature en soustrayant à rel3
l'équation exacte eq et on stocke le résultat dans rel4.
On effectue ensuite des développements en série de Taylor autour de
la solution
. Cette substitution
est faite à la ligne 12 et le résultat est stocké dans la variable
rel3. On calcul l'erreur de troncature en soustrayant à rel3
l'équation exacte eq et on stocke le résultat dans rel4.
On effectue ensuite des développements en série de Taylor autour de
la solution
![]() (lignes 18 à 24), que l'on substitue dans rel4
(ligne 25). L'erreur de troncature est obtenue en l'écrivant sous
forme d'un polynôme en
(lignes 18 à 24), que l'on substitue dans rel4
(ligne 25). L'erreur de troncature est obtenue en l'écrivant sous
forme d'un polynôme en
![]() (ligne 26):
(ligne 26):
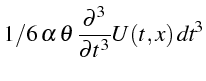 |
|||
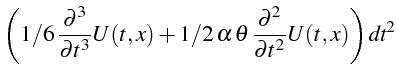 |
|||
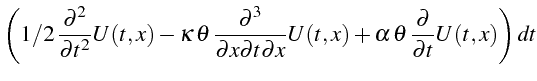 |
|||
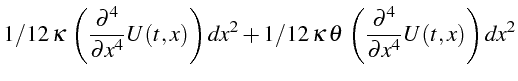 |
On remarque que le coefficient du terme en
![]() ressemble à la dérivée
temporelle de l'équation exacte. On va donc le transformer en utilisant
l'équation exacte. On extrait ce coefficient de la variable ErrT
(ligne 28). On dérive l'équation exacte par rapport à t (ligne 29)
et on la soustraie du coefficient après multiplication par
ressemble à la dérivée
temporelle de l'équation exacte. On va donc le transformer en utilisant
l'équation exacte. On extrait ce coefficient de la variable ErrT
(ligne 28). On dérive l'équation exacte par rapport à t (ligne 29)
et on la soustraie du coefficient après multiplication par
![]() (ligne 30). Le coefficient du terme en
(ligne 30). Le coefficient du terme en
![]() s'écrit alors (ligne
20):
s'écrit alors (ligne
20):
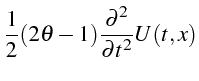
Ce coefficient s'annule pour
![]() .
.
En conclusion le
![]() -schéma (3.5) est consistant
avec l'équation (3.1) et l'erreur de troncature est en
-schéma (3.5) est consistant
avec l'équation (3.1) et l'erreur de troncature est en
![]() sauf pour
sauf pour
![]() (schéma de Crank Nicolson) pour
lequel l'erreur de troncature est en
(schéma de Crank Nicolson) pour
lequel l'erreur de troncature est en
![]() .
.
Le
![]() -schéma s'écrit sous la forme suivante suivante (avec
les paramètres
-schéma s'écrit sous la forme suivante suivante (avec
les paramètres
![]() et
et
![]() donnés en (3.6)):
donnés en (3.6)):
Cette équation n'est évidemment valable que pour les noeuds internes
![]() . Pour les noeuds
. Pour les noeuds
![]() et
et
![]() il faut prendre en compte
les conditions aux limites. En
il faut prendre en compte
les conditions aux limites. En
![]() (
(
![]() ), on a une condition
de Dirichlet, et donc
), on a une condition
de Dirichlet, et donc
En
![]() (
(
![]() ), on a une condition de Neumann, qu'il faut discrétiser
pour calculer
), on a une condition de Neumann, qu'il faut discrétiser
pour calculer
![]() . Pour cela on utilise une condition miroir,
qui consiste à calculer une approximation centrée de la dérivée au
point
. Pour cela on utilise une condition miroir,
qui consiste à calculer une approximation centrée de la dérivée au
point
![]() , pour approximer la valeur manquante
, pour approximer la valeur manquante
![]() à l'aide
de la condition aux limites:
à l'aide
de la condition aux limites:
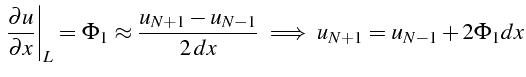
Cela nous permet d'écrire l'équation (3.8) pour
![]() sous
la forme:
sous
la forme:
Les équations (3.8 à 3.10) peuvent s'écrire sous la forme d'un système matriciel:
où
![]() et
et
![]() sont les 2 matrices tridiagonales
suivantes (en notant
sont les 2 matrices tridiagonales
suivantes (en notant
![]() et
et
![]() ):
):
![$\displaystyle \left[\begin{array}{cccccc}
1 & 0 & 0 & & 0 & 0\\
-\theta r & 1+...
...+2r) & -\theta r\\
0 & 0 & 0 & & -2\theta r & 1+\theta(s+2r)\end{array}\right]$](img1162.png) |
|||
![$\displaystyle \left[\begin{array}{cccccc}
1 & 0 & 0 & & 0 & 0\\
\theta_{1}r & ...
...theta_{1}r\\
0 & 0 & 0 & & 2\theta_{1}r & 1-\theta_{1}(s+2r)\end{array}\right]$](img1164.png) |
Nous avons programmé ce
![]() -schéma (3.11), en utilisant
une programmation Matlab optimisée. C'est la fonction tshema
(programme 3.2.6), qui calcule la solution numérique dans
le vecteur T pour une condition initiale T
-schéma (3.11), en utilisant
une programmation Matlab optimisée. C'est la fonction tshema
(programme 3.2.6), qui calcule la solution numérique dans
le vecteur T pour une condition initiale T
![]() ,
des valeurs
,
des valeurs
![]() ,
,
![]() ,
,
![]() et
et
![]() données et un nombre
d'itérations en temps nit fixé. Elle utilise un algorithme
spécifique aux systèmes tri-diagonaux: l'algorithme de Thomas (décrit
dans l'annexe chap3D). C'est un algorithme classique pour
la résolution de systèmes tri-diagonaux, mais il n'est pas implémenté
dans Matlab. Nous avons donc écrit une fonction en language C tridiag
avec une interface Matlab qui est décrite au paragraphe lin3D.
données et un nombre
d'itérations en temps nit fixé. Elle utilise un algorithme
spécifique aux systèmes tri-diagonaux: l'algorithme de Thomas (décrit
dans l'annexe chap3D). C'est un algorithme classique pour
la résolution de systèmes tri-diagonaux, mais il n'est pas implémenté
dans Matlab. Nous avons donc écrit une fonction en language C tridiag
avec une interface Matlab qui est décrite au paragraphe lin3D.
function [T]=tshema(Ti,theta,r,s,phi,nit) % calcul de la solution T du theta-schema % Ti=solution initiale % theta,r,s,phi parametres du shema % nit= nbre de pas d'integration % methode de Thomas avec tridiag N=length(Ti); % matrices 3 Diag e=ones(1,N); A=[-theta*r*e; (1+theta*(2*r+s))*e; -theta*r*e]; C=[(1-theta)*r*e; (1-(1-theta)*(2*r+s))*e; (1-theta)*r*e]; % C.L dirichlet en 1, Neuman en N (cdt miroir) A(:,1)=0; A(2,1)=1; C(:,1)=0; C(2,1)=1; A(1,N)=2*A(1,N); A(3,N)=0; C(1,N)=2*C(1,N); C(3,N)=0; % solution initiale T=Ti; % iterations for it=1:nit B=C(1,1:N)'.*[0;T(1:N-1)]+C(2,1:N)'.*T(1:N)+C(3,1:N)'.*[T(2:N);0]; B(N)=B(N)+phi; T=tridiag(A,B); end
La fonction Matlab tshema (3.2.6) utilise cette
fonction tridiag. Pour cela on construit les matrices tridiagonales
![]() et
et
![]() comme des matrices rectangulaires
comme des matrices rectangulaires
![]() (lignes 10 à 11). On notera aussi la forme du produit matriciel
(lignes 10 à 11). On notera aussi la forme du produit matriciel
![]() (ligne 19) pour le calcul du second membre
(ligne 19) pour le calcul du second membre
![]() .
.
En utilisant cette structure de données et l'algorithme de Thomas
tridiag, on obtiens une méthode très efficace, qui pour
![]() est
est
![]() fois plus rapide que la méthode de Gauss classique implémentée
dans Matlab. On trouvera dans l'annexe chap3D, une comparaison
de l'efficacité des différentes méthodes de résolution de systèmes
tridiagonaux disponibles sous Matlab par rapport à cet algorithme
de Thomas.
fois plus rapide que la méthode de Gauss classique implémentée
dans Matlab. On trouvera dans l'annexe chap3D, une comparaison
de l'efficacité des différentes méthodes de résolution de systèmes
tridiagonaux disponibles sous Matlab par rapport à cet algorithme
de Thomas.
Avec les conditions initiales des cas 1 et 2,
![]() ,
,
![]() ,
,
![]() , on a calculé la solution numérique avec
, on a calculé la solution numérique avec
![]() ,
un maillage de
,
un maillage de
![]() points et
points et
![]() . Le résultat est tracé sur
la figure (3.5). En comparant avec les solutions exactes
(figures 3.3), on constate que l'on a calculé une bonne
approximation de la solution.
. Le résultat est tracé sur
la figure (3.5). En comparant avec les solutions exactes
(figures 3.3), on constate que l'on a calculé une bonne
approximation de la solution.
Pour quantifier l'erreur entre la solution exacte et la solution numérique,
nous allons faire une étude numérique de la précision du
![]() -schéma
pour l'équation de la chaleur (3.1).
-schéma
pour l'équation de la chaleur (3.1).
Pour étudier numériquement la précision du
![]() -schéma (3.11)
, nous avons effectuer deux séries de calcul: une pour déterminer
la précision spatiale et une pour déterminer la précision temporelle.
-schéma (3.11)
, nous avons effectuer deux séries de calcul: une pour déterminer
la précision spatiale et une pour déterminer la précision temporelle.
On a comparé la solution numérique avec la solution analytique (3.4)
au bout d'un temps
![]() (
(
![]() étant le temps caractéristique
de diffusion du problème
étant le temps caractéristique
de diffusion du problème
![]() ). On a choisi un pas
d'intégration
). On a choisi un pas
d'intégration
![]() suffisamment petit pour que l'erreur d'intégration
en temps soit négligeable par rapport à l'erreur spatiale (on a fait
le calcul avec une valeur de
suffisamment petit pour que l'erreur d'intégration
en temps soit négligeable par rapport à l'erreur spatiale (on a fait
le calcul avec une valeur de
![]() fixée et égale à
fixée et égale à
![]() ). On a tracé
sur la figure (3.6a) l'erreur maximale en fonction de
). On a tracé
sur la figure (3.6a) l'erreur maximale en fonction de
![]() pour les 3 valeurs
pour les 3 valeurs
![]() . On vérifie sur la figure
que l'erreur est d'ordre 2 pour tous les schémas (i.e. en
. On vérifie sur la figure
que l'erreur est d'ordre 2 pour tous les schémas (i.e. en
![]() ).
).
[précision spatiale]![\includegraphics[width=0.3\paperwidth,keepaspectratio]{CHAP3/precisdx}](img1177.png) [précision temporelle] [précision temporelle]![\includegraphics[width=0.3\paperwidth,keepaspectratio]{CHAP3/precisdt}](img1178.png)
|
L'étude de la précision temporelle est un peu plus délicate, car il
faut choisir un nombre de points
![]() et des pas en temps
et des pas en temps
![]() tels que l'erreur globale du schéma soit contrôlée par l'erreur d'intégration
en temps. Cela nécessite des calculs avec des pas en temps grands,
qui ne vérifient plus la condition de stabilité du schéma explicite.
Nous avons donc fait l'étude uniquement pour
tels que l'erreur globale du schéma soit contrôlée par l'erreur d'intégration
en temps. Cela nécessite des calculs avec des pas en temps grands,
qui ne vérifient plus la condition de stabilité du schéma explicite.
Nous avons donc fait l'étude uniquement pour
![]() et
et
![]() ,
en comparant la solution analytique (3.4) au bout d'un temps
,
en comparant la solution analytique (3.4) au bout d'un temps
![]() avec la solution calculée numériquement. Pour les
valeurs de
avec la solution calculée numériquement. Pour les
valeurs de
![]() choisies, le paramètre
choisies, le paramètre
![]() varie de
varie de
![]() à
à
![]() , et est donc bien en deçà de la limite de stabilité du schéma
explicite
, et est donc bien en deçà de la limite de stabilité du schéma
explicite
![]() . On a tracé sur la figure (3.6b)
l'erreur maximale en fonction de
. On a tracé sur la figure (3.6b)
l'erreur maximale en fonction de
![]() . On vérifie sur la figure
que le schéma implicite
. On vérifie sur la figure
que le schéma implicite
![]() est d'ordre 1 en temps (i.e.
en
est d'ordre 1 en temps (i.e.
en
![]() ), et que pour les grands
), et que pour les grands
![]() le schéma Cranck
Nicholson
le schéma Cranck
Nicholson
![]() est d'ordre 2 en temps (i.e. en
est d'ordre 2 en temps (i.e. en
![]() ). Pour les petits
). Pour les petits
![]() , on note une saturation
de l'erreur du schéma Cranck Nicholson, qui devient alors contrôlée
uniquement par la précision spatiale.
, on note une saturation
de l'erreur du schéma Cranck Nicholson, qui devient alors contrôlée
uniquement par la précision spatiale.