suivant: 3.5 Écoulement quasi 1D monter: 3. Écoulements compressibles 1D précédent: 3.3 Ondes sonores Table des matières
Les équations d'Euler forment un système hyperbolique, caractéristique d'un phénomène de propagation. Pour étudier les propriétés de ce système, nous considérerons un écoulement compressible instationnaire 1D isentropique. Le système d'équations s'écrit
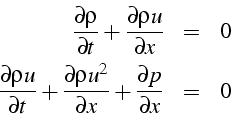
avec la relation isentropique
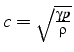 .
.
D'après la relation 3.1, on déduit la relation entre ![]() et
et ![]() :
:
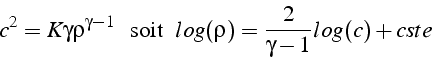
d'où
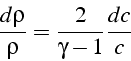
En remplaçant ![]() dans l'équation de bilan de la masse
dans l'équation de bilan de la masse
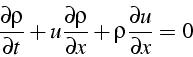
on obtient une équation sur ![]() et
et ![]()
De même en remplaçant dans l'équation de quantité de mouvement:
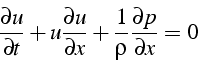
![]() on obtient
on obtient
En additionnant 3.2+3.3 et en soustrayant 3.2-3.3, on obtient les 2 équations caractéristiques:
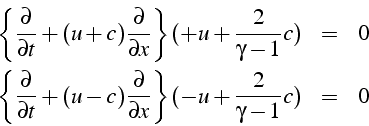
Posons
![]() et
et
![]() (invariants
de Riemann), le système s'écrit:
(invariants
de Riemann), le système s'écrit:
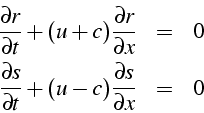
dont l'interprétation est la suivante: soit ![]() la famille
de courbes de pente
la famille
de courbes de pente
![]() et
et ![]() celle de
pente
celle de
pente
![]() , les solutions
, les solutions ![]() et
et ![]() vérifient
vérifient
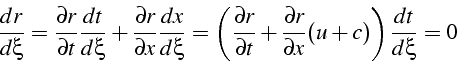
Connaissant les courbes caractéristiques, on peut alors en déduire la solution en tout point.
![\includegraphics[width=0.5\textwidth]{CHAP3/caract}](img435.png)
Soit ![]() un point quelconque du plan
un point quelconque du plan ![]() , il se trouve
à l'intersection de 2 caractéristiques:
, il se trouve
à l'intersection de 2 caractéristiques: ![]() issue de
issue de ![]() et
et ![]() issue de
issue de ![]() . On a donc:
. On a donc:
Connaissant ![]() et
et ![]() on en déduit l'état du fluide en
on en déduit l'état du fluide en ![]() .
.
Cette démarche attractive possède cependant un inconvénient majeur:
on ne sait pas en général déterminer les courbes caractéristiques
![]() et
et ![]() , car elles dépendent de la solution
! Cependant cette approche nous informe sur les propriétés des équations
d'Euler pour un écoulement de gaz:
, car elles dépendent de la solution
! Cependant cette approche nous informe sur les propriétés des équations
d'Euler pour un écoulement de gaz:
Considérons un écoulement d'air se déplaçant à la vitesse ![]() dans un milieu initialement au repos, correspondant au champ de vitesse
initial continu:
dans un milieu initialement au repos, correspondant au champ de vitesse
initial continu:
La répartition de pression et de masse volumique à l'instant initial
est telle que la célérité du son ![]() vérifie:
vérifie:
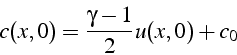
i.e. on a pour ![]() un fluide au repos, avec une pression
un fluide au repos, avec une pression ![]() et une masse volumique
et une masse volumique ![]() t.q.
t.q.
![]() ,
pour
,
pour ![]() un fluide en mouvement à la vitesse
un fluide en mouvement à la vitesse ![]() (avec
(avec
![]() écoulement initial subsonique), avec une pression
écoulement initial subsonique), avec une pression
![]() et une masse volumique
et une masse volumique ![]() t.q.
t.q.
![]() ,
et entre
,
et entre ![]() une transition continue en tangente hyperbolique
une transition continue en tangente hyperbolique
![]() (rq
(rq
![]() ).
).
Avec ces conditions initiales, les invariants de Riemann ont pour valeurs:
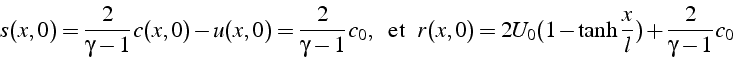
![\includegraphics[width=0.5\textwidth]{CHAP3/caract1}](img461.png)
D'après ce qui précède, ![]() est constant le long des courbes caractéristiques
est constant le long des courbes caractéristiques
![]() qui sont issue de l'axe
qui sont issue de l'axe ![]() . Or
. Or ![]() est constant
à l'instant initial (i.e. sur l'axe
est constant
à l'instant initial (i.e. sur l'axe ![]() ), donc
), donc ![]() doit être constant
dans tout le plan
doit être constant
dans tout le plan ![]()
Pour un point M du plan, on a (voir schéma):
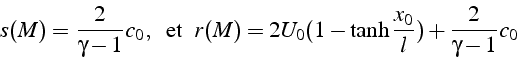
Or d'après la définition de ![]() et
et ![]() on a:
on a:
![]() et
et
![]() ,
, ![]() étant constant dans la plan
et
étant constant dans la plan
et ![]() étant constant le long des courbes
étant constant le long des courbes ![]() , on en déduit
que
, on en déduit
que ![]() et
et ![]() sont forcément constants le long des courbes
sont forcément constants le long des courbes ![]() .
Or les courbes
.
Or les courbes ![]() ont pour pente
ont pour pente ![]() , ce sont donc
des droites. La courbe
, ce sont donc
des droites. La courbe ![]() issue de
issue de ![]() est la droite d'équation
est la droite d'équation
![]() . La famille des droites
. La famille des droites ![]() a pour pente:
a pour pente:
Pour ![]() , la pente devient constante (
, la pente devient constante (
![]() )
et les caractéristiques sont parallèles, et de même pour
)
et les caractéristiques sont parallèles, et de même pour ![]() (la
pente vaut
(la
pente vaut
![]() ). Entre les deux la pente varie continûment
et les courbes caractéristiques
). Entre les deux la pente varie continûment
et les courbes caractéristiques ![]() doivent se rejoindre
au bout d'un temps
doivent se rejoindre
au bout d'un temps ![]() (intersection des droites issues de
(intersection des droites issues de ![]() et
et ![]()
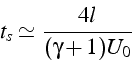
![\includegraphics[width=0.8\textwidth]{CHAP3/caract2}](img473.png)
Or lorsque des caractéristiques de la même famille se coupent, la solution ne peut plus rester continue, et une discontinuité doit apparaıtre. L'hypothèse d'écoulement isentropique n'est plus vérifiée et on a apparition d'un choc de compression.
Les courbes caractéristiques ont pour équation (avec les notations 3.5):
On a montré que ![]() était constant le long de ces caractéristiques,
donc
était constant le long de ces caractéristiques,
donc
![]()
Connaissant la solution initiale ![]() 3.4, on en
déduit la solution
3.4, on en
déduit la solution ![]()
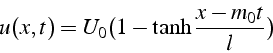
et la solution ![]()
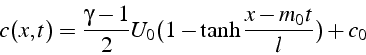
On note que ![]() (3.5) vérifie:
(3.5) vérifie:
La solution est donc une onde qui se propage à la vitesse absolue
![]() , c'est à dire à la vitesse
, c'est à dire à la vitesse ![]() relativement au fluide.
La vitesse de propagation des perturbation par rapport au fluide est
donc bien
relativement au fluide.
La vitesse de propagation des perturbation par rapport au fluide est
donc bien ![]() , la célérité du son locale. Pour une perturbation
faible
, la célérité du son locale. Pour une perturbation
faible
![]() , on retrouve l'approximation de l'acoustique
avec des ondes se propageant avec une célérité constante
, on retrouve l'approximation de l'acoustique
avec des ondes se propageant avec une célérité constante ![]() .
.
Cette analyse est confirmée par une résolution numérique des équations d'Euler, dont la solution au cours du temps est tracée ci dessous.
![\includegraphics[width=0.7\textwidth]{CHAP3/euler1}](img483.png)
Si on considère une onde de détente, i.e. une perturbation correspondant à un champ de vitesse opposé au précédent:
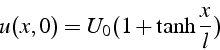
la perturbation s'évanouit au cours du temps, puisque les courbes caractéristiques divergent (voir figure ci dessous)
![\includegraphics[width=0.6\textwidth]{CHAP3/euler2}](img485.png)