3.3 Ondes sonores

On considère une perturbation de pression $p'(x,t)$ dans un écoulement d'air stationnaire en moyenne ($U_{0},$ $p_{0},\rho_{0}$). Cette perturbation induit une perturbation de masse volumique $\rho'$ et de vitesse $u'$. La pression $p_{0}+p'$ , la masse volumique $\rho_{0}+\rho'$ et la vitesse $\textrm{U}_{0}+u'$ sont solutions des équations d'Euler. De plus les fluctuations étant faibles, l'écoulement est isentropique et on néglige les fluctuations devant les valeurs moyennes $U_{0},\rho_{0}$ et $p_{0}$ en ne conservant que les termes d'ordre 1.

En se plaçant dans un référentiel en translation uniforme $U_{0}$, la fluctuation $p'$ est solution de l'équation des ondes:

$$\frac{\partial^{2}p'}{\partial t^{2}}-\frac{\gamma p_{0}}{\rho_{0}}\frac{\partial^{2}p}{\partial x^{2}}=0$$

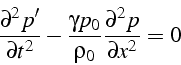
La fluctuation de vitesse $u'$ est définie par:

$$\frac{\partial u'}{\partial t}=-\frac{1}{\rho_{0}}\frac{\partial p'}{\partial x}$$

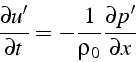
et la fluctuation de masse volumique $\rho'$:

$$\rho'=\frac{\rho_{0}}{\gamma}\frac{p'}{p_{0}}$$

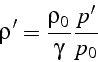
Cette équation des ondes décrit la propagation d'une onde de pression $p'(x,t)$ avec une célérité $c_{0}=\sqrt{\gamma p_{0}/\rho_{0}}$ . La solution générale de cette équation est de la forme

$$p'(x,t)=F(x-c_{0}t)+G(x+c_{0}t)$$

Les fonctions $F$ et $G$ sont déterminées par les conditions initiales $p'(x,0)$ et $\frac{\partial p'}{\partial t}(x,0)$

Ainsi pour une perturbation sinusoıdale $p'(x,t)=Be^{i\omega(x-c_{0}t)}$, la fluctuation de vitesse $u'$ vaut $u'(x,t)=\frac{1}{\rho_{0}c_{0}}Be^{i\omega(x-c_{0}t)}$, et la fluctuation de masse volumique $\rho'(x,t)=\frac{1}{c_{0^{2}}}Be^{i\omega(x-c_{0}t)}$.

3.3.0.1 Ordre de grandeurs

Dans de l'air au repos $\rho_{0}=1\, kg/m^{3}$ , $p_{0}=10^{5}\, Pa$ , $\gamma=1.4$ on a $c_{0}=370\, m/s$

Les ondes de pression ont une puissance acoustique de l'ordre de 1 à 100 db. La puissance acoustique en décibel est liée à la puissance moyenne $w'$ de l'onde par la relation:

$$db=120+10\, log_{10}(w')$$

et la puissance moyenne $w'$ est donné par:

$$w'=\frac{\omega c_{0}}{2\pi}\int_{0}^{\frac{\omega c_{0}}{2\pi}}p'(x,t).\overline{u'(x,t)}\, dt=\frac{B^{2}}{\rho_{0}c_{0}}$$

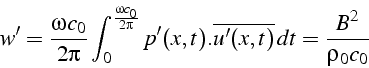
Cela donne l'ordre de grandeurs des amplitudes $B$ des ondes de pression: $B=10^{-4}\, Pa$ à $1\, Pa$, de l'amplitude des fluctuations de vitesse $0.3\,10^{-6}\, m/s$ à $0.3\,10^{-2}\, m/s$ et de l'amplitude des fluctuations de masse volumique $0.9\,10^{-9}\, kg/m^{3}$ à $0.9\,10^{-5}\, kg/m^{3}$. On constate donc que les ondes sonores sont quasiment incompressibles. De plus le déplacement $\xi$ des particules est très faible. En effet l'équation de la trajectoire d'une particule s'écrit:

$$\frac{d\xi}{dt}=u'(\xi,t)\,\, avec\,\,\xi(0)=x$$

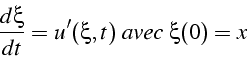
En linéarisant l'équation, i.e. en approximant $u'(\xi,t)=u'(x,t)$ , on intègre cette équation:

$$\xi=\frac{iB}{\rho_{0}\omega c_{0}^{2}}e^{i\omega(x-c_{0}t)}=\frac{1}{2\pi f}\frac{iB}{\rho_{0}c_{0}}e^{i\omega(x-c_{0}t)}$$

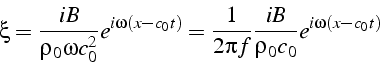
en notant $f=\frac{\omega c_{0}}{2\pi}$ la fréquence temporelle de l'onde. Pour des ondes acoustiques ( $f=10\, hz$ à $10\, khz$), avec $f=330\, hz$ on obtient une amplitude du déplacement de $0.4\,10^{-9}\, m$ à $0.4\,10^{-5}\, m$.

3.3.0.2 Exemple de propagation d'une onde sonore

3.3.0.3 Cône de Mach

On considère l'émission de perturbations (ondes sonores) par une source. Différents cas se présentent suivant que la source se déplace à une vitesse supérieure ou inférieure à la vitesse de propagation des ondes: i.e. la vitesse du son. (voir animations)

1. Si la source est immobile $U_{0}=0$, les surfaces d'ondes sont des sphères
   
   

   

2. Si $U_{0}<c_{0}$ (écoulement subsonique)
   
   

   

3. Si $U_{0}=c_{0}$ (écoulement transsonique)
   
   

   

4. si $U_{0}>c_{0}$ (écoulement supersonique)
   
   

   

Dans ce dernier cas, la source se déplace plus vite que l'onde, qui reste contenu dans un cône à l'arrière de la source, que l'on appelle cône de Mach. Le demi angle au sommet $\alpha$ du cône vérifie:

$$sin\,\alpha=\frac{c_{0}}{u_{0}}=Ma^{-1}$$

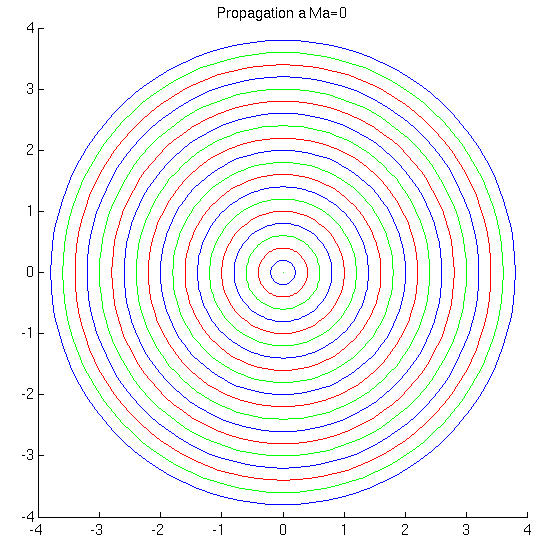
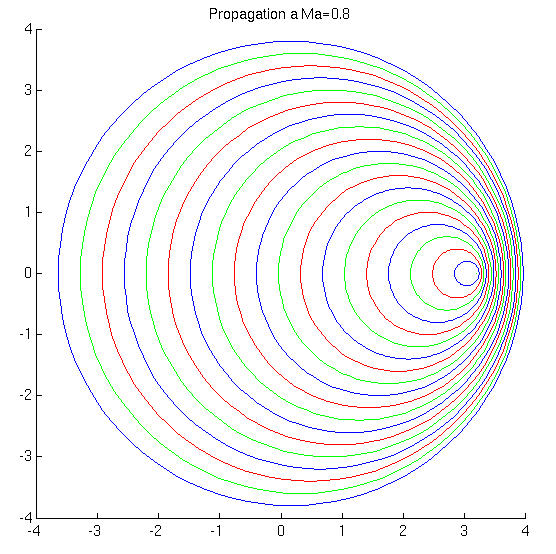
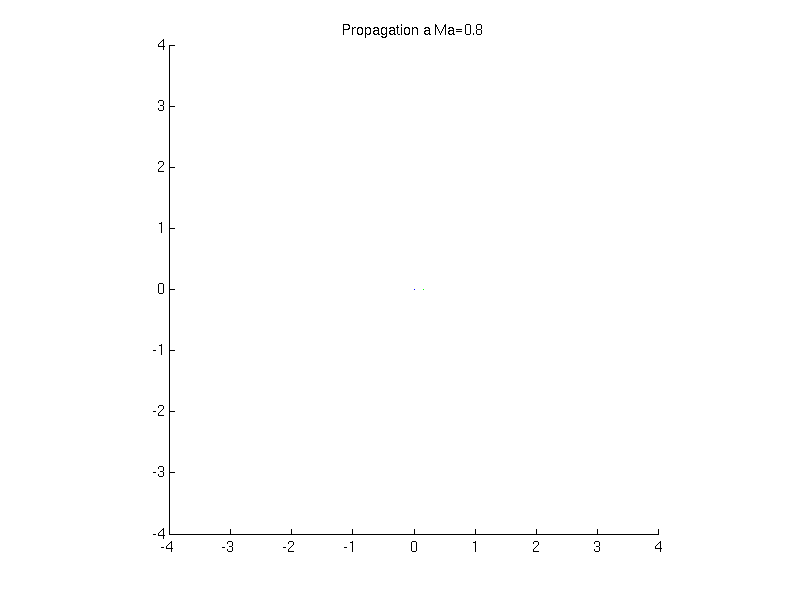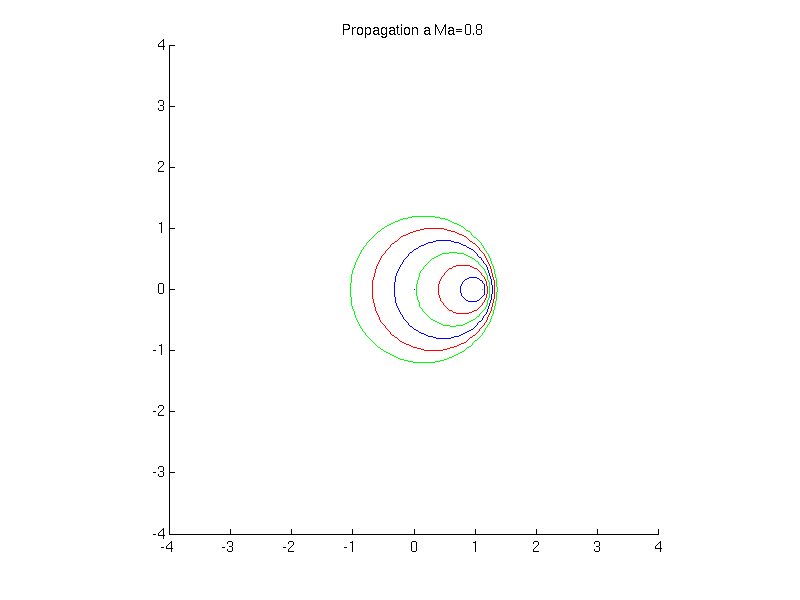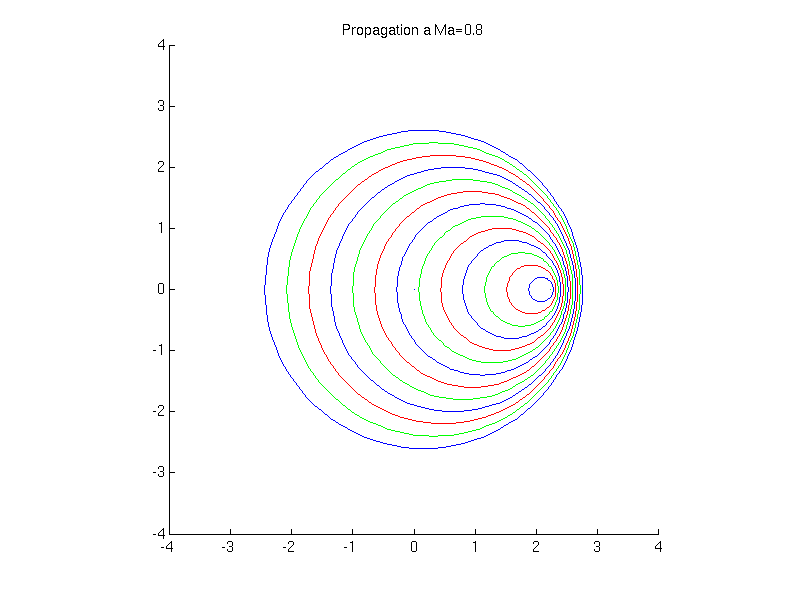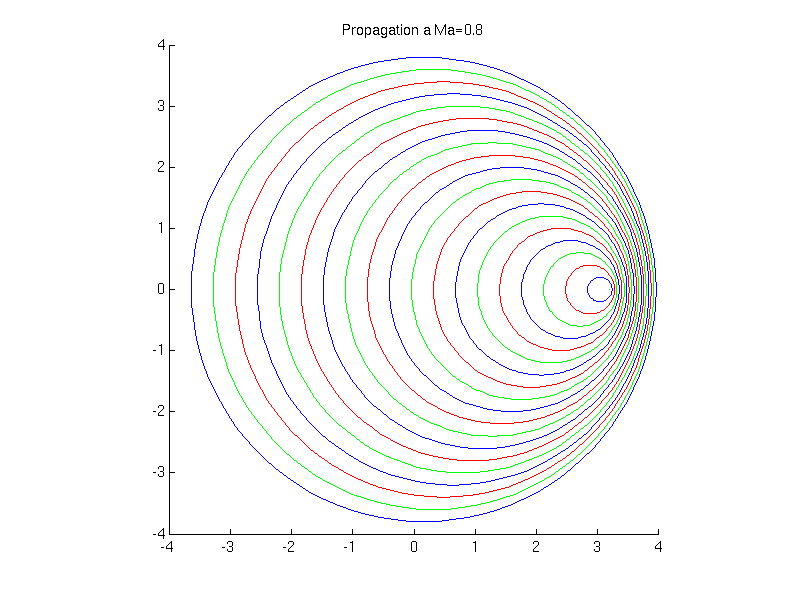
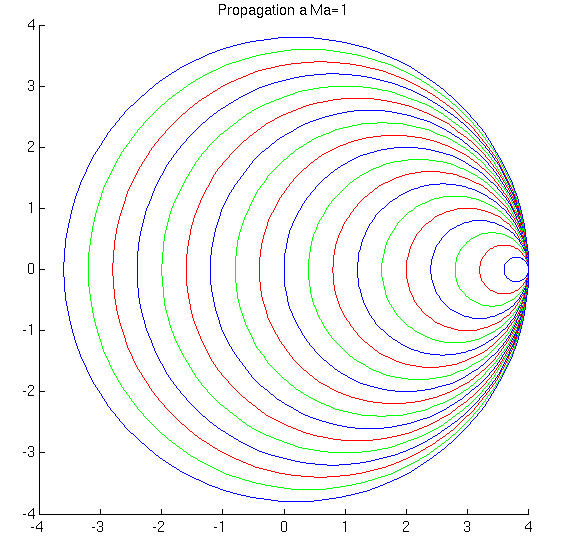
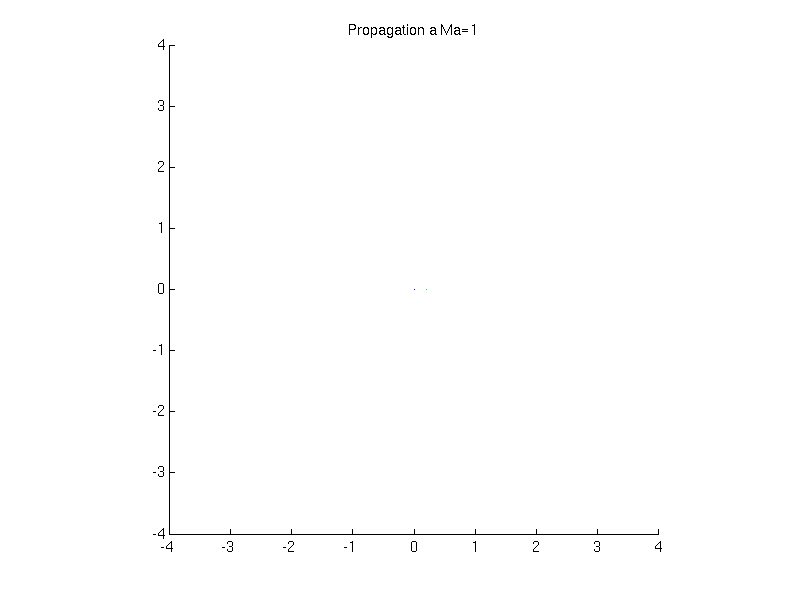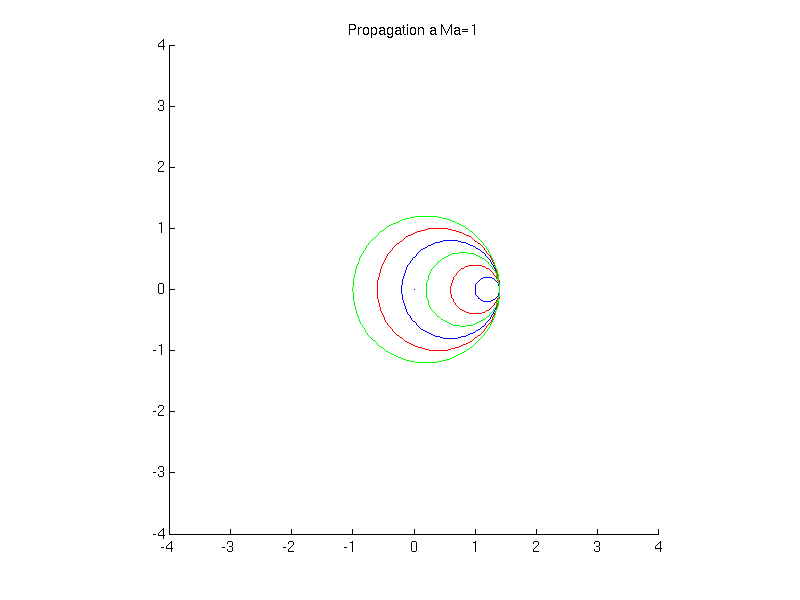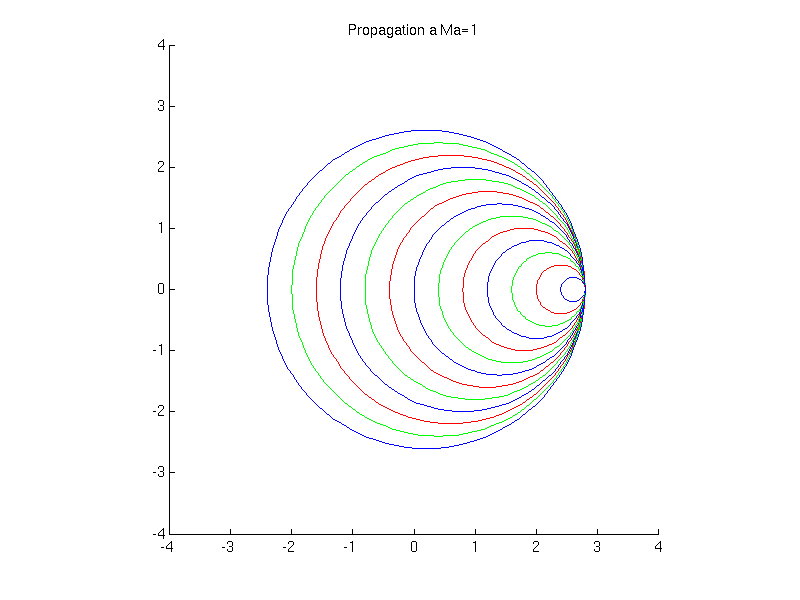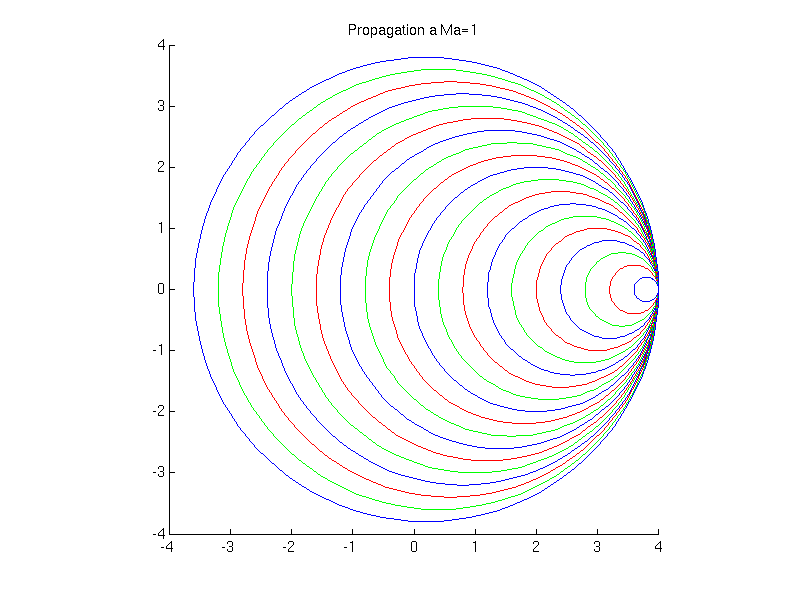
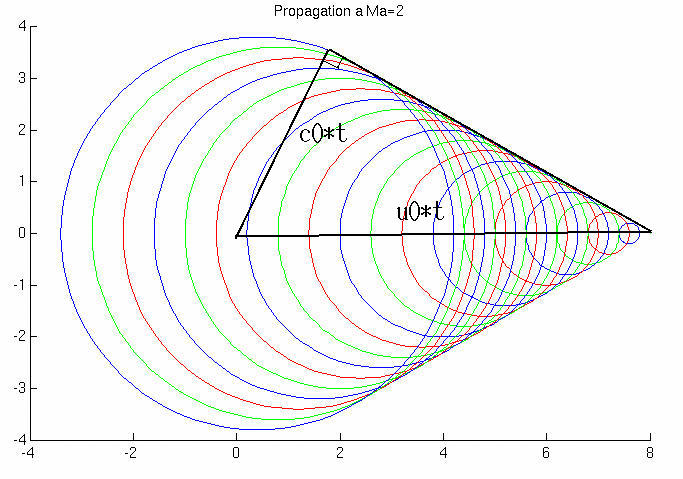
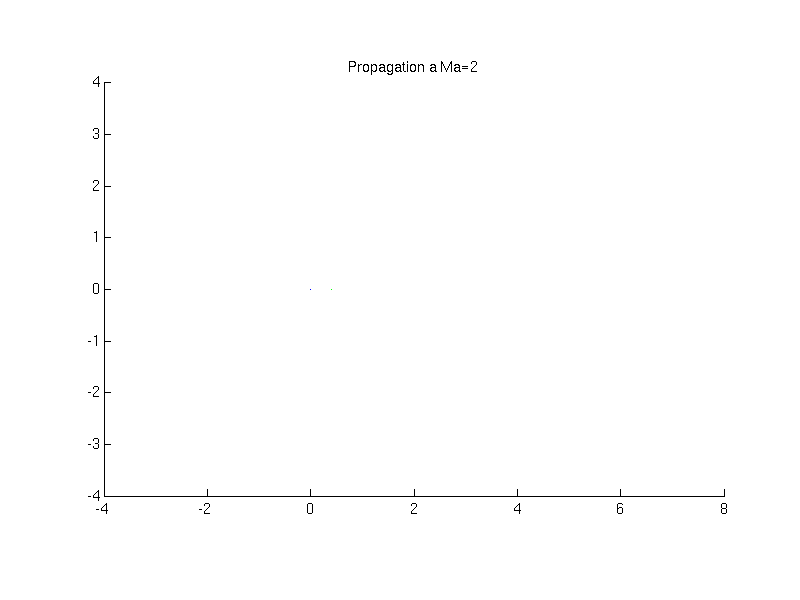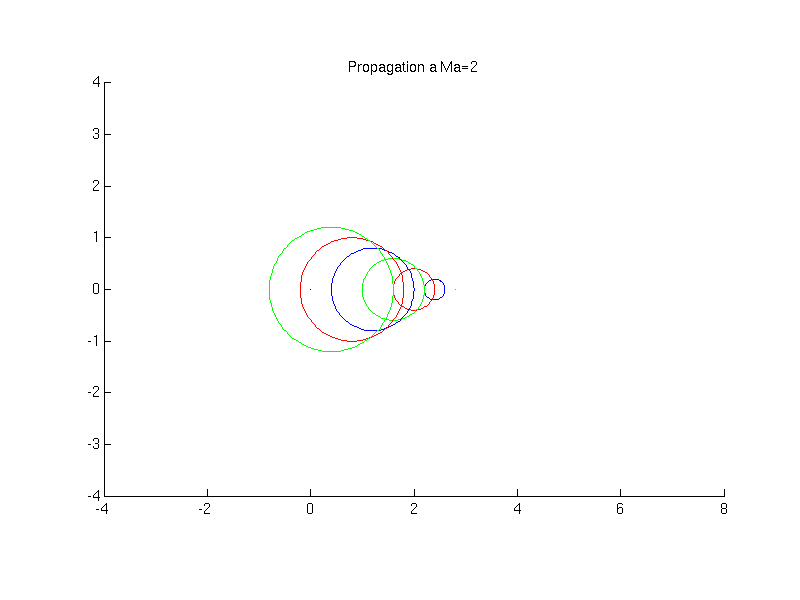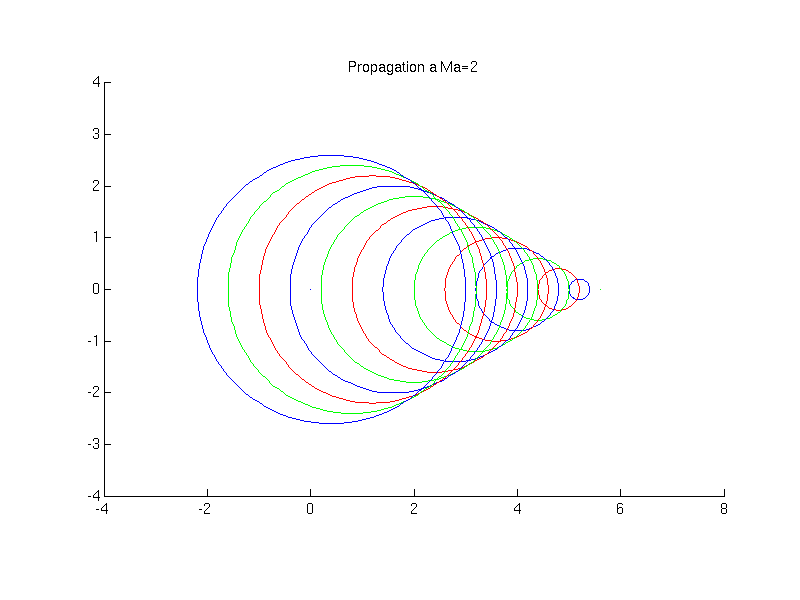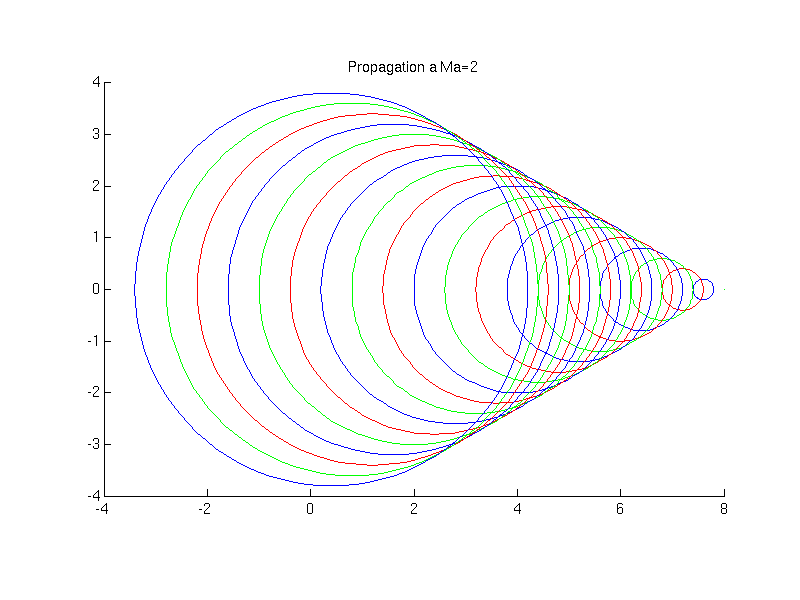
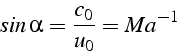
Cet angle est inversement proportionnel au nombre de Mach $Ma=\frac{u_{0}}{c_{0}}$

Dans l'animation suivante, on modélise le champ de pression généré par un dipôle harmonique se déplaçant à une vitesse supersonique constante. On visualise le champ de pression généré par le dipôle.

Animation Video AVI Cinepak