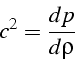suivant: 3.3 Ondes sonores monter: 3. Écoulements compressibles 1D précédent: 3.1 Ecoulement 1D Table des matières
Considérons tout d'abord la propagation d'une perturbation de pression
![]() dans un tuyau de section constante contenant un gaz au repos.
Cette onde sonore se propage avec une célérité
dans un tuyau de section constante contenant un gaz au repos.
Cette onde sonore se propage avec une célérité ![]() . L'apparition
d'une perturbation de pression engendre une augmentation
. L'apparition
d'une perturbation de pression engendre une augmentation ![]() de
la vitesse du gaz, perturbation qui se propage aussi à la célérité
de
la vitesse du gaz, perturbation qui se propage aussi à la célérité
![]() Considérons un volume de contrôle
Considérons un volume de contrôle ![]() qui suit le front de
la perturbation
qui suit le front de
la perturbation ![]() (figure ci dessous)
(figure ci dessous)
![\includegraphics[width=0.6\textwidth]{CHAP3/front}](img337.png)
Ce volume de contrôle se déplace à la vitesse ![]() par rapport à un
référentiel fixe et l'écoulement relatif peut être considéré comme
stationnaire en temps. Donc dans la section
par rapport à un
référentiel fixe et l'écoulement relatif peut être considéré comme
stationnaire en temps. Donc dans la section ![]() après le front (fluide
au repos), la vitesse relative vaut
après le front (fluide
au repos), la vitesse relative vaut ![]() , la pression
, la pression ![]() et la masse volumique
et la masse volumique ![]() et dans la section
et dans la section ![]() avant le front,
la vitesse relative du fluide vaut
avant le front,
la vitesse relative du fluide vaut ![]() , la pression
, la pression ![]() et la masse volumique
et la masse volumique ![]() .
.
L'équation de bilan de la masse intégrée entre ![]() et
et ![]() s'écrit:
s'écrit:
d'où au premier ordre l'accroissement de vitesse:
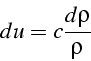
De la même façon l'équation de bilan de la quantité de de mouvement
intégrée entre ![]() et
et ![]() s'écrit:
s'écrit:
et en ne conservant que les termes au premier ordre
et en remplaçant ![]() , on obtient- l'expression de la célérité de
l'onde de pression:
, on obtient- l'expression de la célérité de
l'onde de pression:
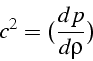
Cette expression de la célérité des ondes est en fait générale (i.e. ne dépend pas du type de gaz), à condition de noter que l'expression trouvée suppose des petites perturbations (i.e. un écoulement isentropique). Dans ce cas, on a pour un gaz :
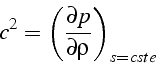
Pour un gaz parfait, on a montré que l'écoulement isentropique vérifiait
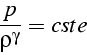
ce qui nous donne l'expression de la célérité des ondes dans un gaz parfait
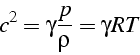
qui dépend donc de ![]() . Pour de l'air à température ambiante
. Pour de l'air à température ambiante
![]() ,
, ![]() ,
, ![]() la vitesse du son vaut
la vitesse du son vaut ![]()
Remarque: pour un écoulement isentropique, on peut remplacer l'équation de bilan de l'énergie par la relation (valable pour n'importe quel gaz):