suivant: 4. Ondes de Choc monter: 3. Écoulements compressibles 1D précédent: 3.4 Équations caractéristiques Table des matières
On considère un écoulement quasi-1D dans une conduite de section ![]() variable. On suppose que la variation de section
variable. On suppose que la variation de section ![]() est suffisamment
faible pour que l'écoulement soit uni-dimensionnel avec une vitesse
est suffisamment
faible pour que l'écoulement soit uni-dimensionnel avec une vitesse
![]() .
.
![\includegraphics[width=0.6\textwidth]{CHAP3/conduite}](img488.png)
On considère le volume de contrôle ![]() de la figure ci-dessus, limité
par les sections
de la figure ci-dessus, limité
par les sections ![]() et
et ![]()
Les équations de bilan d'un gaz parfait compressible (voir chapitre
1) intégrées sur le volume ![]() de frontière
de frontière ![]() s'écrivent
(après utilisation du théorème de la divergence):
s'écrivent
(après utilisation du théorème de la divergence):
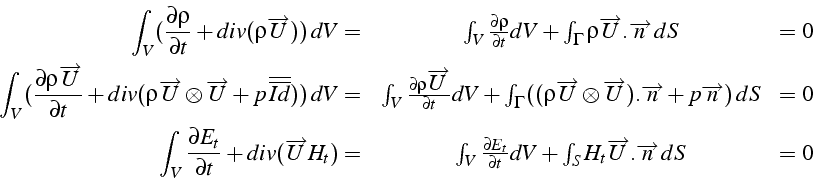
On a noté
![]() l'énergie totale par
unité de volume, et
l'énergie totale par
unité de volume, et ![]() l'enthalpie totale.
l'enthalpie totale.
A ces équations, on rajoute l'équation d'état des gaz parfaits:
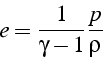
Le volume ![]() considéré est égal au premier ordre en x à
considéré est égal au premier ordre en x à
![]() ,
donc les intégrales de volume d'une fonction
,
donc les intégrales de volume d'une fonction ![]() s'écrivent:
s'écrivent:
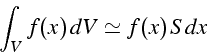
Les intégrales de surface d'une fonction ![]() se décomposent en
intégrale sur les sections débitantes
se décomposent en
intégrale sur les sections débitantes ![]() et
et ![]() , et sur
la frontière pariétale
, et sur
la frontière pariétale ![]() :
:
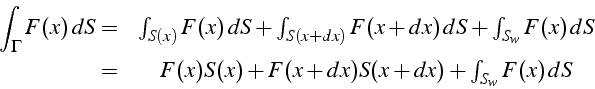
Pour l'équation de bilan de la masse,
![]() est nulle sur les frontières pariétales et vaut
est nulle sur les frontières pariétales et vaut ![]() en
en
![]() et
et ![]() en
en ![]() (la normale
(la normale
![]() est toujours dirigée vers l'extérieur du volume de contrôle). On obtient
alors:
est toujours dirigée vers l'extérieur du volume de contrôle). On obtient
alors:
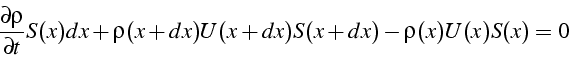
soit au premier ordre en x:
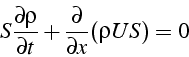
Pour l'équation de bilan de quantité de mouvement, ![]()
est la composante suivant ![]() qui est non nulle sur les frontières
pariétales et vaut
qui est non nulle sur les frontières
pariétales et vaut ![]() où
où
![]() est la composante suivant
est la composante suivant ![]() de la normale à la frontière. L'intégrale
sur la paroi s'écrit au premier ordre en x:
de la normale à la frontière. L'intégrale
sur la paroi s'écrit au premier ordre en x:
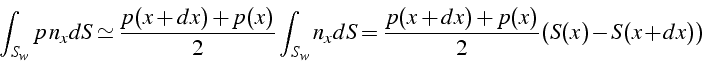
Sur ![]() ,
, ![]() vaut
vaut ![]() et sur
et sur ![]()
![]() vaut
vaut ![]() , et l'équation de bilan de la quantité de mouvement
s'écrit:
, et l'équation de bilan de la quantité de mouvement
s'écrit:
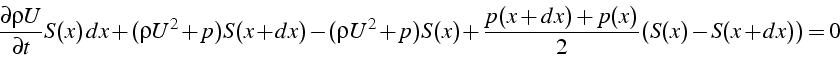
ce qui donne au premier ordre en x:
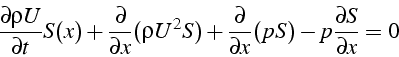
soit:
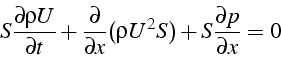
Enfin l'équation de bilan de l'énergie,
![]() qui s'annulle sur les parois et vaut
qui s'annulle sur les parois et vaut ![]() en
en ![]() et
et ![]() en
en ![]() , ce qui donne au final:
, ce qui donne au final:
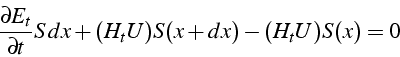
soit à l'ordre 1 en x:
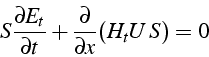
Les équations de bilan pour un gaz parfait dans une conduite de section
![]() s'écrivent donc:
s'écrivent donc:
avec l'équation d'état:
![]()
Dans le cas d'un écoulement stationnaire, le système d'équations (3.6-3.8) se simplifie.
L'équation de bilan de la masse 3.6 s'écrit:
i.e. le débit massique (i.e. en kg/s) se conserve .
L'équation de bilan de l'énergie 3.8 s'écrit:
En notant
![]() l'enthalpie totale par unité
de masse, on obtient:
l'enthalpie totale par unité
de masse, on obtient:
i.e. l'enthalpie totale par unité de masse se conserve.
Pour l'équation de bilan de la quantité de mouvement 3.7, on obtient (en utilisant 3.6):
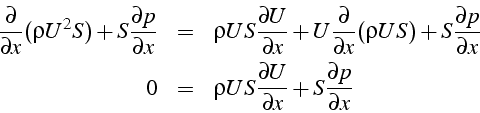
ce qui se simplifie
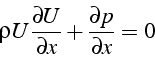
Sous forme différentielle, on peut l'écrire:
![]() .
.
Le système d'équation pour un écoulement permanent en conduite s'écrit
auquel on adjoint l'équation d'état
![]()
Dans le cas où l'écoulement ne présente pas de discontinuité (choc), l'écoulement est aussi isentropique (exercice).
En prenant le logarithme de l'équation 3.9 , on obtient:
soit en différenciant:
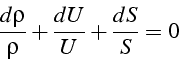
En utilisant l'équation 3.11 pour remplacer ![]() , on a:
, on a:
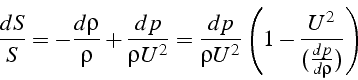
En introduisant la célérité du son
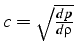 , et
le nombre de Mach local
, et
le nombre de Mach local ![]() , l'équation précédente s'écrit:
, l'équation précédente s'écrit:
Interprétons cette relation et ces conséquences si on veut accélérer un gaz:
Nous allons maintenant étudier le moyen de générer un écoulement supersonique à l'aide d'une tuyère convergente-divergente, dite tuyère de Laval. Ce dispositif est très utilisé pour étudier expérimentalement les écoulements supersoniques.
![\includegraphics[width=0.6\textwidth]{CHAP3/laval}](img554.png)
On considère un réservoir, contenant un gaz à la pression ![]() et à la température
et à la température ![]() , relié à une sortie qui est à une pression
, relié à une sortie qui est à une pression
![]() et une température
et une température ![]() par une conduite convergente
divergente de section
par une conduite convergente
divergente de section ![]() , dont la valeur minimum vaut
, dont la valeur minimum vaut ![]() au col.
au col.
Le réservoir est suffisamment grand pour considérer que la vitesse
du fluide y est négligeable (![]() ). Le fluide est quasiment
au repos et donc dans des conditions d'arrêt: pression d'arrêt
). Le fluide est quasiment
au repos et donc dans des conditions d'arrêt: pression d'arrêt ![]() et température d'arrêt
et température d'arrêt ![]() .
.
En supposant que l'écoulement est stationnaire et isentropique dans la tuyère, les lois de bilan s'écrivent:
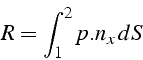
Nous allons tout d'abord déterminer les relations entre l'état générateur
(conditions d'arrêt) et l'état dans une section ![]() quelconque
de la conduite (en supposant un écoulement isentropique entre les
deux).
quelconque
de la conduite (en supposant un écoulement isentropique entre les
deux).
La conservation de l'enthalpie totale 3.13 permet d'obtenir
une relation entre les températures, en notant que l'enthalpie pour
un gaz parfait s'écrit ![]()
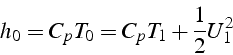
soit
en introduisant la vitesse du son
![]() , la
relation
, la
relation ![]() et le nombre de Mach local
et le nombre de Mach local ![]() .
.
En utilisant la relation isentropique
![]() , qui s'écrit en fonction de
, qui s'écrit en fonction de ![]() :
:
![]() ,
on obtiens l'évolution de la masse volumique:
,
on obtiens l'évolution de la masse volumique:
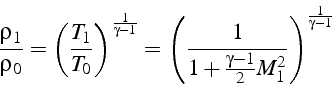
et l'évolution de la pression:
L'évolution de ces quantités est donnée sur la figure ci-dessous:
![\includegraphics[width=0.52\textwidth]{CHAP3/relarret}](img577.png)
L'évolution de l'écoulement isentropique à partir de condition d'arrêt
correspond donc à une diminution de la température, i.e. à la transformation
de l'enthalpie (énergie interne + pression) en énergie cinétique.
En effectuant un développement limité en nombre de Mach au voisinage
de ![]() , on obtient les expressions suivantes:
, on obtient les expressions suivantes:
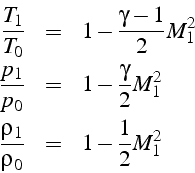
On constate que les variations relatives à faible nombre de Mach sont
proportionnelles à ![]() , et sont négligeables pour
, et sont négligeables pour ![]() (moins de
(moins de ![]() ). A température ambiante
). A température ambiante ![]() , un nombre
de Mach
, un nombre
de Mach ![]() correspond donc à une vitesse de
correspond donc à une vitesse de ![]() soit
soit ![]() . Cela justifie l'hypothèse d'écoulement incompressible
. Cela justifie l'hypothèse d'écoulement incompressible
![]() pour des vitesses telles que
pour des vitesses telles que ![]() .
.
ATTENTION: pour un écoulement incompressible, la masse volumique,
la pression et la température sont constantes dans l'équation de bilan
de masse et d'énergie (les fluctuations sont négligeables). Par contre
dans l'équation de bilan de quantité de mouvement le terme en gradient
de pression
![]() doit être conservé, car
il est du même ordre que le terme d'inertie
doit être conservé, car
il est du même ordre que le terme d'inertie
![]() . Ce sont en effet les fluctuations de pression (dites fluctuations
dynamiques) qui génèrent l'écoulement. Par contre ces fluctuations
sont négligeables devant la pression totale (pression thermodynamique),
ce qui permet de considérer les propriétés thermodynamiques d'un fluide
incompressible comme constantes.
. Ce sont en effet les fluctuations de pression (dites fluctuations
dynamiques) qui génèrent l'écoulement. Par contre ces fluctuations
sont négligeables devant la pression totale (pression thermodynamique),
ce qui permet de considérer les propriétés thermodynamiques d'un fluide
incompressible comme constantes.
Étudions l'évolution de la quantité de mouvement ![]() dans
la tuyère. Pour cela exprimons
dans
la tuyère. Pour cela exprimons ![]() en fonction du nombre de Mach
en fonction du nombre de Mach
![]() , de
, de ![]() et de
et de ![]()
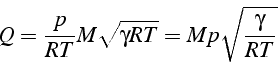
en remplaçant ![]() et
et ![]() en fonction des conditions d'arrêt (3.14,
3.15)
en fonction des conditions d'arrêt (3.14,
3.15)
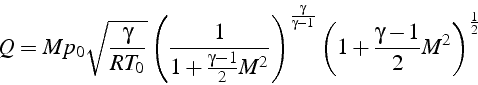
soit
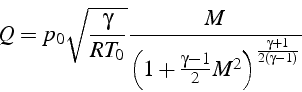
Si la tuyère est adaptée, l'écoulement est sonique au col ![]() ,
et la quantité de mouvement au col
,
et la quantité de mouvement au col ![]() est obtenue en faisant
est obtenue en faisant
![]() dans l'expression précédente
dans l'expression précédente
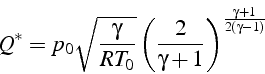
d'où le rapport
![]() qui est aussi le
rapport des sections d'après la conservation de la masse:
qui est aussi le
rapport des sections d'après la conservation de la masse:
Cette relation permet de définir l'évolution du nombre de Mach en fonction de la section de la tuyère.
![\includegraphics[width=0.5\textwidth]{CHAP3/machtuyere}](img599.png)
On constate que pour une section donnée, on a deux nombres de Mach
possibles, un Mach supersonique ou un Mach subsonique. Donc pour une
tuyère de Laval adaptée, on a 2 écoulements possibles. En effet dans
la partie convergente, l'écoulement est forcément subsonique (puisqu'on
part d'un écoulement au repos). Par contre dans la partie divergente,
l'écoulement peut être soit subsonique, soit supersonique suivant
la valeur de la pression en sortie de tuyère. En effet ayant la valeur
du nombre de Mach, la relation 3.15 nous fournit la pression
correspondante. Sur la figure ci-dessous on a tracé l'évolution des
quantités ![]() pour une tuyère parabolique et pour les 2
types d'écoulements possibles.
pour une tuyère parabolique et pour les 2
types d'écoulements possibles.
![\includegraphics[width=0.4\textwidth]{CHAP3/tuyere1}](img601.png)
![\includegraphics[width=0.4\textwidth]{CHAP3/tuyere2}](img602.png)
On constate que si la pression de sortie (en ![]() ,i.e.
,i.e.
![]() ) vaut
) vaut
![]() l'écoulement reste subsonique
dans la tuyère et sonique au col, par contre si la pression vaut
l'écoulement reste subsonique
dans la tuyère et sonique au col, par contre si la pression vaut
![]() ,
alors l'écoulement est supersonique dans la partie divergente.
,
alors l'écoulement est supersonique dans la partie divergente.
Si la pression en sortie ![]() est supérieure à
est supérieure à ![]() , alors l'écoulement
n'est plus sonique au col et reste subsonique dans la tuyère.
, alors l'écoulement
n'est plus sonique au col et reste subsonique dans la tuyère.
Si la pression en sortie ![]() est comprise entre
est comprise entre ![]() et
et ![]() , alors l'écoulement n'est plus isentropique et on montrera que dans
ce cas un choc se produit dans la tuyère.
, alors l'écoulement n'est plus isentropique et on montrera que dans
ce cas un choc se produit dans la tuyère.
Enfin si la pression en sortie est inférieure à ![]() , alors
en sortie l'écoulement n'est plus isentropique et un choc en sortie
apparaıt.
, alors
en sortie l'écoulement n'est plus isentropique et un choc en sortie
apparaıt.