1.6 Equation de bilan d'énergie

Les différentes forme d'énergie (par unité de volume) dans un gaz sont:

• l'énergie cinétique: $\frac{1}{2}\rho U^{2}$
• l'énergie potentielle: $\rho gz$
• l'énergie interne: E (énergie cinétique interne des molécules)

L'énergie interne par unité de volume $E=\rho e$ (où $e$ est l'énergie interne par unité de masse) est une variable d'état thermodynamique, ( i.e. qui est fonction de deux autres variables d'état, par exemple $E=E(T,\rho)$) dont la variation est donnée par le premier principe de la thermodynamique:

$$d\, E=\underbrace{\Delta W}_{\mbox{travail\, fournit\, par\, compression}}+\underbrace{\Delta Q}_{\mbox{flux\, de\, chaleur}}$$

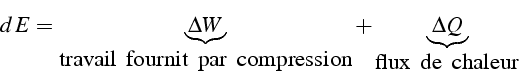
Le travail élémentaire fournit au gaz par une compression de $dV$ du volume s'écrit:

$$\Delta W=-p\, dV$$

Le flux de chaleur correspond à la diffusion de la chaleur dans le gaz, le rayonnement, l'échauffement visqueux. En général ce flux de chaleur est irréversible. Dans le cas d'une transformation réversible (lente), le flux de chaleur est relié à la variation d'entropie $S$:

$$\Delta Q=T\, dS$$

Le second principe de la thermodynamique implique, que pour une transformation quelconque:

$$dS\,\geq\frac{\Delta Q}{T}$$

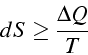
Dans les écoulements que nous considérons, nous négligerons les flux de chaleur, i.e. nous supposerons l'écoulement adiabatique. Nous avons donc:

$$d\, E=-p\, dV\,\,\mbox{\, et\, }\,\, dS\geq0$$

Pour l'élément de fluide de la figure 1.1, la variation d'énergie interne pendant $\Delta t$ est égale au travail de compression sur les facettes:

$$\frac{\Delta E}{\Delta t}=\frac{\Delta\rho e}{\Delta t}dxdyd... ...n}_{3}+\overrightarrow{U}_{4}.\overrightarrow{n}_{4}\right)dxdz$$

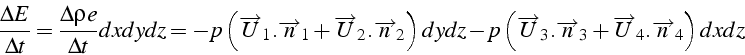
soit après un développement limité à l'ordre 1

$$\frac{\Delta\rho e}{\Delta t}dxdydz=-p\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)dxdydz$$

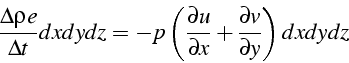
ce qui s'écrit :

$$\frac{\partial\rho e}{\partial t}+div(\rho e\overrightarrow{U})=-p\, div(\overrightarrow{U})$$

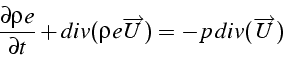
En développant et en utilisant l'équation de bilan de masse, il vient:

$$\rho\underbrace{\left(\frac{\partial e}{\partial t}+\overrig... ...t}}=-\underbrace{p\, div(\overrightarrow{U})}_{-p\frac{dV}{dt}}$$

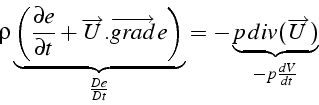
En ajoutant l'équation de bilan sur l'énergie cinétique, on obtient une équation de bilan sur l'énergie totale:

$$\rho\frac{D}{Dt}(e+\frac{1}{2}U^{2})=-p\, div(\overrightarrow{U})-\overrightarrow{U}.\overrightarrow{grad}\, p$$

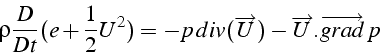
soit:

$$\rho\left(\frac{\partial(e+\frac{1}{2}U^{2})}{\partial t}+\o... ...ow{grad}\,(e+\frac{1}{2}U^{2})\right)=-div(p\overrightarrow{U})$$

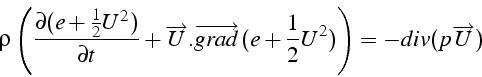
qui s'écrit sous forme conservative

$$\frac{\partial}{\partial t}(\rho e+\frac{1}{2}\rho U^{2})+div((\rho e+\frac{1}{2}\rho U^{2}+p)\overrightarrow{U})=0$$

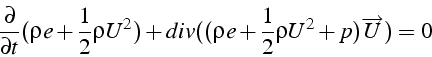
Le terme $e+\frac{1}{2}U^{2}=e_{t}$ représente l'énergie totale par unité de masse. Le terme $h=e+\frac{p}{\rho}$ correspond à l'enthalpie par unité de masse, et le terme $h+\frac{1}{2}U^{2}=e+\frac{p}{\rho}+\frac{1}{2}U^{2}=h_{t}$ l'enthalpie totale par unité de masse.

Remarque: nous avons négligé les flux de chaleur $\Delta Q$ dans les écoulements considérés, qui sont une des causes de l'irréversibilité, mais cela n'implique pas que les écoulements considérés soient réversibles (en particulier à cause des chocs). Cependant dans certaines régions l'écoulement peut être considéré comme réversible. Dans ce cas, d'après le premier principe, on a par unité de volume:

$$de=T\, dS-p\, d\frac{1}{\rho}$$

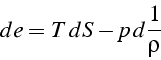
soit pour une particule fluide:

$$\rho T\frac{DS}{Dt}=\rho\frac{De}{Dt}-\frac{p}{\rho}\frac{D\rho}{Dt}$$

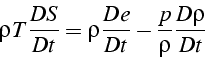
ce qui nous donne l'évolution de l'entropie $S$ (en utilisant l'équation de bilan de masse):

$$\rho T\frac{DS}{Dt}=-p\, div\overrightarrow{U}+p\, div\overrightarrow{U}=0$$

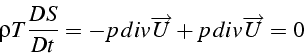
Dans un écoulement réversible, les particules fluides ont donc une entropie $S$ constante, i.e. l'entropie se conserve le long des trajectoires.