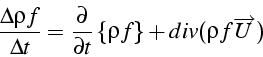1.3 Equations de bilan

Pour simplifier l'exposé, nous allons considérer un écoulement bidimensionnel plan(i.e. dont les propriétés ne varient pas suivant z, et dont la composante de vitesse suivant z est nulle). On choisit un élément de volume dessiné sur la figure 1.1 de cotés dx et dy , et d'épaisseur dz.

Figure 1.1: élément de contrôle

La vitesse du fluide $\overrightarrow {U}(x,y,t)$ est différente suivant les faces de l'élément:

$$\overrightarrow{U_{1}}=\overrightarrow{U}(x-\frac{dx}{2},y,t... ...\,\overrightarrow{U_{4}}=\overrightarrow{U}(x,y+\frac{dy}{2},t)$$

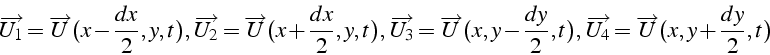
Soit $f(x,y,t)$ une grandeur physique du fluide par unité de volume, l'équation de bilan associée s'écrit sous la forme générale suivante:

$$\underbrace{\frac{\Delta(\rho f)}{\Delta t}}_{\mbox{variatio... ...lément}}=\underbrace{S}_{\mbox{somme\, des\, termes\, sources}}$$

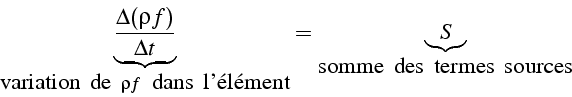
Dans une description eulérienne, la variation de $\rho f$ est due d'une part à la variation temporelle de $\rho f$ dans l'élément:

$$\left\{ \rho f(t+dt,x,y,z)-\rho f(t,x,y,z)\right\} dxdydz=\frac{\partial}{\partial t}\left\{ \rho f\right\} dtdxdydz$$

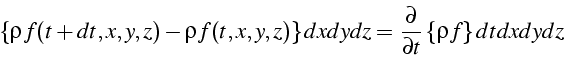
et d'autre part au bilan des flux $\Delta F$ de $\rho f$ à travers les faces de l'élément.

Pour une facette de surface $dS$, de normale $\overrightarrow{n}$, sur laquelle la vitesse du fluide est égale à $\overrightarrow{U}$, le flux $F$ de $\rho f$ à travers la facette (i.e. la quantité de $f$ qui passe à travers la facette pendant $dt$ ) s'écrit:

$$F=\rho f*\underbrace{((\overrightarrow{U}.\overrightarrow{n})dt*dS)}_{\mbox{volume\, traversant\, la\, facette}}$$

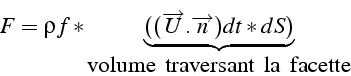
Le bilan des flux sur l'élément s'écrit donc en faisant le bilan sur les facettes de l'élément (en tenant compte du fait que l'écoulement est bidimensionnel plan et donc $\overrightarrow{U}.\overrightarrow{n}=0$ sur les facettes $z-\frac{dz}{2}$ et $z+\frac{dz}{2}$). Ce bilan s'écrit avec les notations de la figure 1.1:

$$\Delta F=\rho_{1}f_{1}\overrightarrow{U_{1}}.\overrightarrow... ...rho_{4}f_{4}\overrightarrow{U_{4}}.\overrightarrow{n_{4}}dtdxdz$$

avec

$$\begin{eqnarray*} \rho_{1}f_{1}=\rho f(x-\frac{dx}{2},y,t), & \overrightarrow{n}... ...verrightarrow{U_{4}}.\overrightarrow{n_{4}}=v(x,y-\frac{dy}{2},t)\end{eqnarray*}$$

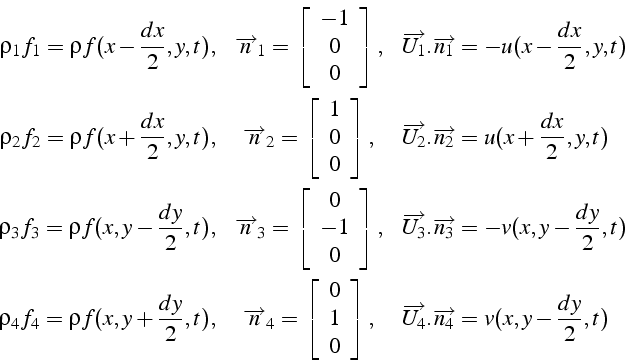
ce qui donne en regroupant les termes:

$$\begin{eqnarray*} \Delta F & = & \left\{ \rho f(x+\frac{dx}{2},y,t)*u(x+\frac{dx... ...)-\rho f(x,y-\frac{dy}{2},t)*v(x,y-\frac{dy}{2},t)\right\} dtdxdz\end{eqnarray*}$$

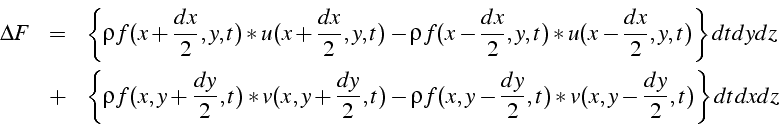
En effectuant un développement limité, et en ne conservant que les termes au premier ordre (les termes d'ordre supérieure ont une contribution qui tend vers zero), il vient:

$$\Delta F=\left\{ \frac{\partial}{\partial x}(\rho fu)+\frac{... ...\rho fv)\right\} dtdxdydz=div(\rho f\overrightarrow{U})dtdxdydz$$

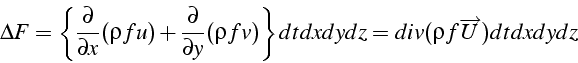
La variation de $\rho f$ pendant $\Delta t$ dans l'élément $dxdydz$ s'écrit donc de façon générale (en 2D et 3D):

$$\frac{\Delta\rho f}{\Delta t}\, dxdydz=\underbrace{\frac{\pa... ...div(\rho f\overrightarrow{U})dxdydz}_{\mbox{flux\, surfacique}}$$

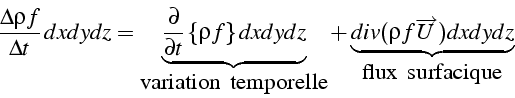
qui s'écrit aussi en divisant par le volume élémentaire:

$$\frac{\Delta\rho f}{\Delta t}=\frac{\partial}{\partial t}\left\{ \rho f\right\} +div(\rho f\overrightarrow{U})$$