suivant: 1.5 Equation de bilan monter: 1. Description d'un gaz précédent: 1.3 Equations de bilan Table des matières
Puisqu'il n'y a pas création de masse, la variation de masse
![]() dans l'élément
dans l'élément ![]() est nulle
est nulle
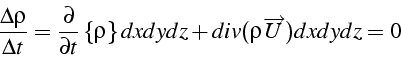
ce qui s'écrit après simplification (forme conservative)
soit
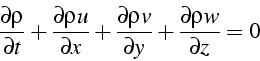
En décomposant, on obtient la forme non-conservative ou convective
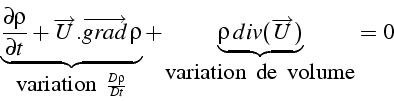
On note que
![]() représente la variation de
volume du fluide par unité de temps:
représente la variation de
volume du fluide par unité de temps:
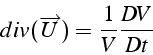
![\includegraphics[width=0.2\textwidth]{CHAP1/div}](img193.png)
L'équation de conservation de la masse s'écrit donc (en suivant le mouvement d'une particule fluide) :
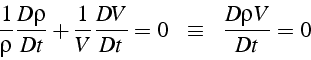
On a une interprétation mécanique de l'équation (1.1),
qui traduit: “la masse ![]() d'une particule fluide est
constante”. La variation de la masse volumique d'une
particule fluide est due à la variation de son volume.
d'une particule fluide est
constante”. La variation de la masse volumique d'une
particule fluide est due à la variation de son volume.
Si le fluide est incompressible, la masse volumique d'une particule fluide est constante, i.e.:
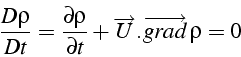
Son volume est donc constant, et on en déduit que le champ de vitesse d'un fluide incompressible doit être à divergence nulle: