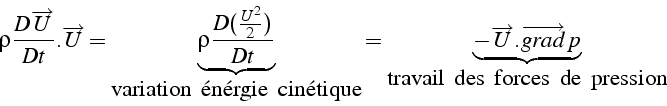1.5 Equation de bilan de quantité de mouvement

La loi fondamentale de la dynamique: la variation de la quantité de mouvement dans l'élément $dxdydz$ est égale à la somme des efforts appliqués

$$\frac{\Delta\rho\overrightarrow{U}}{\Delta t}=\sum\overrightarrow{F}$$

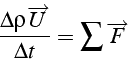
Les efforts extérieurs appliqués sur l'élément sont:

• des forces volumiques: la gravité $\overrightarrow{g}\rho dxdydz$, les forces éléctro-magnétiques, ...
• des forces surfaciques: interaction des autres particules fluides sur l'élément

Pour un fluide ces forces surfaciques sont:

• des forces normales de pression: $-p\overrightarrow{n}dS$ (qui existent même pour un fluide au repos)
• des forces de viscosité (tenseur) $\overrightarrow{\sigma}\otimes\overrightarrow{n}dS$ (qui dépendent du tenseur des déformations $\frac{\partial U_{i}}{\partial x_{j}}$)

Pour les écoulements de gaz étudiés (écoulement à grande vitesse), la force de gravité est très faible et on négligera les effets de viscosité (couches limites, sillage, ..).

Avec ces approximations, la somme des forces de pression s'écrit pour l'élément de la figure 1.1:

$$\sum\overrightarrow{F}=\left(p(x-\frac{dx}{2},y,t)-p(x+\frac... ...{2},t)-p(x,y+\frac{dy}{2},t)\right)dxdz\,\overrightarrow{e_{y}}$$

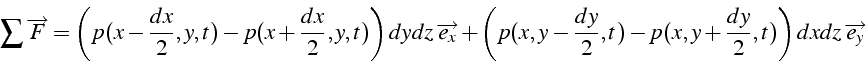
En effectuant un développement limité à l'ordre 1, on obtient:

$$\sum\overrightarrow{F}=-\frac{\partial p}{\partial x}dxdydz\... ...x}}-\frac{\partial p}{\partial y}dxdydz\,\overrightarrow{e_{y}}$$

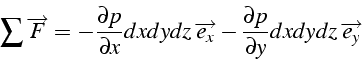
ce qui conduit à l'équation de bilan de quantité de mouvement:

$$\frac{\Delta\rho\overrightarrow{U}}{\Delta t}=\frac{\partial... ...dydz=\sum\overrightarrow{F}=-\overrightarrow{grad}\, p\, dxdydz$$

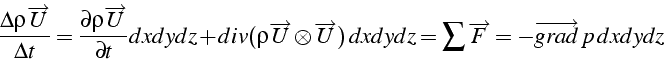
soit sous forme vectorielle (forme conservative)

$$\frac{\partial\rho\overrightarrow{U}}{\partial t}+div(\rho\o... ...htarrow{U}\otimes\overrightarrow{U})=-\overrightarrow{grad}\, p$$

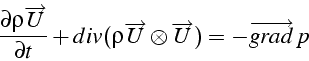
qui correspond aux 3 équations scalaires en coordonnées cartésiennes:

$$\begin{eqnarray*} \frac{\partial\rho u}{\partial t}+div(\rho u\overrightarrow{U}... ...l t}+div(\rho w\overrightarrow{U})=-\frac{\partial p}{\partial z}\end{eqnarray*}$$

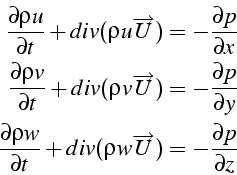
On peut écrire une forme conservative complète en notant $\overline{\overline{Id}}$ le tenseur identité $\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right]$:

$$\frac{\partial\rho\overrightarrow{U}}{\partial t}+div(\rho\o... ...rrow{U}\otimes\overrightarrow{U}+p\,\overline{\overline{Id}})=0$$

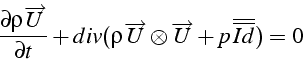
La forme non conservative (ou convective) s'obtient en développant le terme en divergence et en utilisant l'équation de bilan de masse:

$$\begin{eqnarray*} \frac{\partial\rho u}{\partial t}+div(\rho u\overrightarrow{U}... ...w{U}.\overrightarrow{grad}\, u\right)\\ & = & \rho\frac{Du}{Dt}\end{eqnarray*}$$

L'équation sous forme non conservative correspond donc à l'écriture classique de la loi fondamentale de la dynamique: $m\overrightarrow{\gamma}=\overrightarrow{F}$:

$$\rho\frac{D\overrightarrow{U}}{Dt}=\rho\left(\frac{\partial\... ...row{grad}\,\overrightarrow{U}\right)=-\overrightarrow{grad}\, p$$

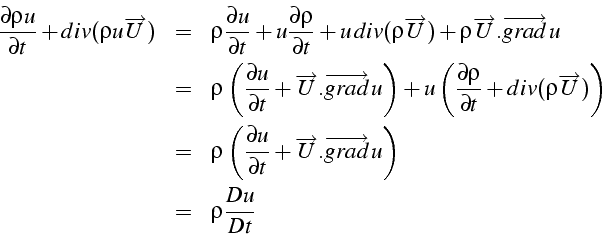
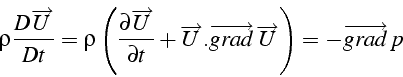
De cette équation, on peut en déduire une équation de bilan sur l'énergie cinétique en effectuant le produit scalaire avec le vecteur vitesse $\overrightarrow{U}$

$$\rho\frac{D\overrightarrow{U}}{Dt}.\overrightarrow{U}=\under... ...rrow{grad}\, p}_{\mbox{travail\, des\, forces\, de\, pression}}$$