suivant: 1.3 Equations de bilan monter: 1. Description d'un gaz précédent: 1.1 Expérience préliminaire Table des matières
Un fluide en mouvement est définit par des grandeurs physiques:
Pour décrire l'évolution de ces grandeurs, on ne choisit pas de suivre les particules fluides dans leur mouvement (description lagrangienne où l'observateur se déplace avec le même mouvement que les particules).
On choisit une approche eulérienne où l'observateur est à une position
fixe et regarde passer les particules fluides. Pour écrire les équations
de bilan, on choisit un élément de volume ![]() situé à une abscisse
situé à une abscisse
![]() dans un repère fixe. Les grandeurs physiques dépendent
alors du point d'observation
dans un repère fixe. Les grandeurs physiques dépendent
alors du point d'observation
![]() et du temps
et du temps
![]() :
:
Si on suit cette description, l'observateur verra passé les particules
fluides. Si on veut suivre une particule M (dont la position est ![]() à t=0) au cours du temps, on calculera sa trajectoire, qui est tangente
à chaque instant au vecteur vitesse:
à t=0) au cours du temps, on calculera sa trajectoire, qui est tangente
à chaque instant au vecteur vitesse:
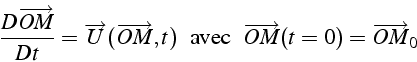
A un instant ![]() fixé, on peut calculer les lignes de courant
de l'écoulement qui sont les lignes
fixé, on peut calculer les lignes de courant
de l'écoulement qui sont les lignes ![]() tangentes en chaque
point au vecteur vitesse.
tangentes en chaque
point au vecteur vitesse.
ATTENTION: lignes de courant et trajectoires sont en général différentes sauf pour un écoulement stationnaire (dont les propriétés ne dépendent pas du temps).
Pour calculer l'accélération d'une particule, on doit suivre cette
particule: on note ![]() la dérivée particulaire ( i.e.
le long de la trajectoire), et
la dérivée particulaire ( i.e.
le long de la trajectoire), et
![]() les dérivées partielles eulériennes (i.e. en un point fixe de l'espace):
les dérivées partielles eulériennes (i.e. en un point fixe de l'espace):
![\begin{eqnarray*}
\overrightarrow{\gamma}= & \frac{D\overrightarrow{^{2}OM}}{Dt^...
...overrightarrow{grad}v\\
\overrightarrow{grad}w\end{array}\right]\end{eqnarray*}](img163.png)