1.7 Equations d'Euler

Les équations précédentes forme le système des équations d'Euler qui régissent les écoulements de gaz parfaits adiabatiques (i.e. dans lesquel on a négligé les effets de viscosité et de transfert de chaleur).

Ce système s'écrit sous forme conservative

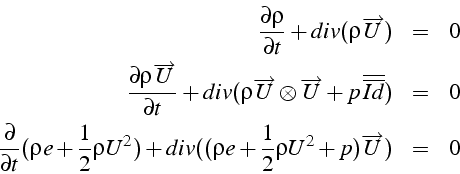
$$\begin{eqnarray*} \frac{\partial\rho}{\partial t}+div(\rho\overrightarrow{U}) & ... ...)+div((\rho e+\frac{1}{2}\rho U^{2}+p)\overrightarrow{U}) & = & 0\end{eqnarray*}$$

où $\overline{\overline{Id}}$ est le tenseur identité

Sous une forme cartésienne indicielle, ces équations deviennent:

$$\begin{eqnarray*} \frac{\partial\rho}{\partial t}+\frac{\partial\rho U_{i}}{\par... ...ial(\rho e+\frac{1}{2}\rho U^{2}+p)U_{i}}{\partial x_{i}} & = & 0\end{eqnarray*}$$

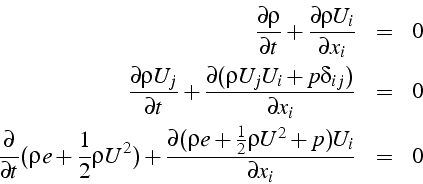
Pour un écoulement bidimensionnel, elles se développent suivant:

$$\begin{eqnarray*} \frac{\partial\rho}{\partial t}+\frac{\partial\rho u}{\partial... ...tial(\rho e+\frac{1}{2}\rho(u^{2}+v^{2})+p)v}{\partial y} & = & 0\end{eqnarray*}$$

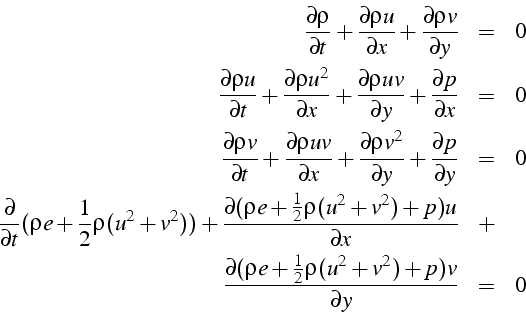
Ces 5 (4 en 2D) équations de bilan lient l'évolution des 6 (5 en 2D) propriétés $\rho,p,e,\overrightarrow{U}$ du gaz. Il manque donc une relation pour fermer le système: c'est l'équation d'état du fluide.