suivant: 1.9 Résumé du chapitre monter: 1. Description d'un gaz précédent: 1.7 Equations d'Euler Table des matières
On montre en théorie cinétique des gaz que les propriétés thermodynamiques
d'un gaz sont fonctione de 2 quantités moléculaires: la masse volumique
et le module de la vitesse des molécules. Donc les propriétés thermodynamiques
sont déterminées par deux variables d'état, les autres étant déterminées
par une équation d'état. On doit donc avoir ![]()
Pour un gaz parfait (air par exemple), l'équation d'état s'écrit:
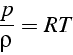
où ![]() est une constante qui dépend de la composition moléculaire
du gaz:
est une constante qui dépend de la composition moléculaire
du gaz:
où ![]() est la constante universelle des gaz parfait
est la constante universelle des gaz parfait
![]() et
et ![]() la masse molaire du gaz (en
la masse molaire du gaz (en ![]() ). Pour l'air, on a
). Pour l'air, on a ![]() ,
d'où la valeur de la constante
,
d'où la valeur de la constante ![]() de l'air:
de l'air:
De plus l'énergie interne ![]() par unité de masse ne dépend que de
la température:
par unité de masse ne dépend que de
la température: ![]() . En notant
. En notant ![]() la chaleur spécifique
à volume constant:
la chaleur spécifique
à volume constant:
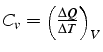 ,
on a
,
on a
Pour un gaz qualorifiquement parfait (air à température usuelle),
![]() est constante et on a:
est constante et on a:
D'où la relation entre ![]()
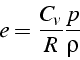
Cette relation peut être simplifiée en introduisant ![]() , la
chaleur spécifique à pression constante:
, la
chaleur spécifique à pression constante:
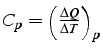 qui
vérifie:
qui
vérifie:
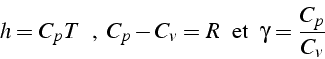
Le rapport des chaleurs spécifiques est constant et vaut ![]() pour un gaz diatomique (air). D'où l'expression de
pour un gaz diatomique (air). D'où l'expression de ![]()
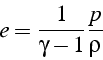
On peut déduire l'expression de l'entropie ![]() d'un gaz parfait,
en utilisant la relation du premier principe pour une petite variation
réversible:
d'un gaz parfait,
en utilisant la relation du premier principe pour une petite variation
réversible:
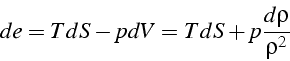
soit
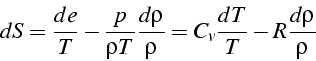
Or d'après l'équation d'état
![]() ,
,
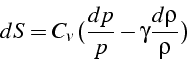
qui après intégration donne:
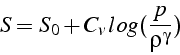
On en déduit que pour un fluide isentropique (i.e.
![]() ), on a
), on a
![]()