construction de BVH optimal, SAH et parcours efficace

Construire un arbre BVH permet d'accélérer l'intersection d'un rayon avec un ensemble de triangles, cf le lancer de rayons, ça rame ? ou pas ?, en évitant de calculer toutes les intersections. La solution proposée dans le tuto précédent est correcte, mais il existe de nombreuses manières de répartir un ensemble de triangles en 2 sous-groupes pour construire les fils de chaque noeud de l'arbre... et certaines seront plus efficaces que d'autres...

par exemple, on peut trier les triangles le long d'un axe et répartir la première moitiée dans le fils gauche et l'autre dans le fils droit, au lieu de couper l'englobant spatialement au milieu et de répartir les triangles entre les fils du noeud en fonction de leur position par rapport au milieu de l'englobant, comme suggéré dans le lancer de rayons, ça rame ? ou pas ?.

Comment comparer ces deux solutions et comment choisir la meilleure ?

il est bien sur possible de constuire les 2 arbres et de vérifier leur efficacité :

• solution 1 : trier les triangles et répartir chaque moitiée dans un fils, construction BVH 0.6s, rendu 28s,

  int build_node( const int begin, const int end )
  {
      assert(begin < end);
      
      // construire l'englobant des triangles
      BBox bounds= triangle_bounds(begin, end);
      
      if(end - begin <= 2)                            
      {
          // il ne reste plus qu'un ou 2 triangles,
          // construire une feuille et renvoyer son indice
          int index= nodes.size();
          nodes.push_back( make_leaf(bounds, begin, end) );
          return index;
      }
      
      // axe le plus etire de l'englobant
      int axis= bounds.max();
      
      // trier les triangles sur l'axe
      std::sort(triangles.data() + begin, triangles.data() + end, triangle_less(axis));
      
      // repartir les triangles et construire les fils du noeud
      int m= (begin + end) / 2;
      int left= build_node(begin, m);
      int right= build_node(m, end);
      
      // construire le noeud
      int index= nodes.size();
      nodes.push_back( make_node(bounds, left, right) );
      return index;
  }

• solution 2 : répartir les triangles dans chaque fils en fonction de leur position dans l'englobant, construction BVH 0.1s, rendu 10s,

  int build_node( const int begin, const int end )
  {
      assert(begin < end);
      
      // construire l'englobant des triangles
      BBox bounds= triangle_bounds(begin, end);
      if(end - begin <= 2)                            
      {
          // il ne reste plus qu'un ou 2 triangles,
          // construire une feuille et renvoyer son indice
          int index= nodes.size();
          nodes.push_back( make_leaf(bounds, begin, end) );
          return index;
      }
      
      // construire l'englobant des centres des triangles
      BBox cbounds= centroid_bounds(begin, end);
      // axe le plus etire de l'englobant des centres des triangles
      int axis= cbounds.max(); 
      
      // repartir les triangles 
      auto *p= std::partition(triangles.data() + begin, triangles.data() + end, 
          centroid_less(axis, cbounds.centroid(axis));
      int m= std::distance(triangles.data(), p);
      
      if(m == begin || m == end)              // l'englobant est degenere, forcer une repartition...
          m= (begin + end) / 2;
      
      // repartir les triangles et construire les fils du noeud
      int left= build_node(begin, m);
      int right= build_node(m, end);
      
      // construire le noeud
      int index= int(nodes.size());
      nodes.push_back( make_node(bounds, left, right) );
      return index;
  }    

• solution 3 : ?? construction BVH 0.8s, rendu 8s.

La solution 1 construit un arbre équilibré, la moitiée des triangles est affectée à chaque fils, la solution 2 par contre, construit un arbre déséquilibré, mais qui est plus rapide à parcourir...

pourquoi ? si on suppose que les triangles [begin .. end] sont répartis uniformement dans l'englobant :

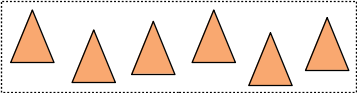
il n'y aura pas vraiment de différence entre les 2 solutions :

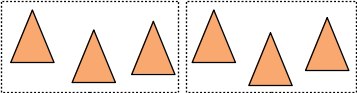
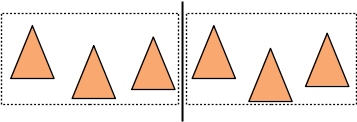
par contre, si les triangles ne sont pas répartis de manière uniforme dans l'englobant :

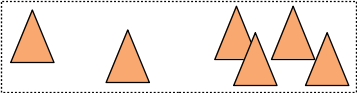
la solution 1 et la solution 2 ne vont pas du tout construire les mêmes noeuds / répartir les triangles de la même façon. La solution 1 place les 3 premiers triangles (les plus à gauche) dans le fils gauche et les 3 suivants (les plus à droite) dans le fils droit du noeud :

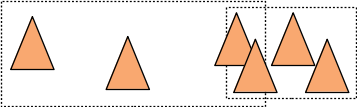
et les englobants des fils se chevauchent et sont aussi plus "gros" que les englobants construits par la solution 2 qui construit un arbre plus rapide à parcourir pour les rayons...

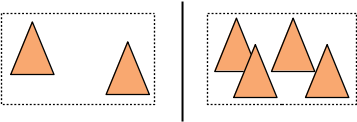
Et intuitivement si l'englobant d'un noeud est plus gros, on peut s'attendre à ce que plus de rayons le visite / le traverse... Si les englobants des fils d'un noeud se chevauchent, on peut aussi s'attendre à ce que les rayons visitent tous les fils du noeud, ce qui n'est probablement pas très efficace...

La solution 3, compare plusieurs répartitions et choisit la meilleure pour construire chaque noeud... la construction est plus longue, mais permet de gagner du temps sur le calcul de l'image. Mais il va falloir cogiter un peu pour évaluer si une répartition est interessante ou pas...

Géométrie et probabilité

On peut résumer notre problème à cette question : "pour N rayons qui traversent un noeud, combien visitent chaque fils ?", ou : "pour N rayons qui traversent un englobant, combien traversent l'englobant d'un fils ??"...

De manière assez surprenante, la réponse à cette question est très simple, c'est un des premiers résultats de la géométrie intégrale.

Pour 2 englobants, (P)ère et (F)ils, avec F inclut dans P, comme les englobants d'un père et d'un fils, si N droites uniformes traversent le noeud P, alors \( \frac{aire(F)}{aire(P)} N\) droites traversent le fils F... ou interprété différement :

\[ \frac{aire(F)}{aire(P)} \]

représente le nombre de fois ou le fils est visité (si le père est visité). et c'est assez logique : plus un englobant est gros, plus il sera visité lors du parcours de l'arbre...

Ces notions sont définies plus précisement dans :
"Some Integral Geometry Tools to Estimate the Complexity of 3D Scenes", F. Cazals, M. Sbert, 1997.

et si A et B sont les fils de P, \( \frac{aire(A)+aire(B)}{aire(P)} \in [0 .. 2]\) représente le nombre de fils visité en moyenne.
(remarque : on obtient bien 2 lorsque les fils A et B font la même taille que P)

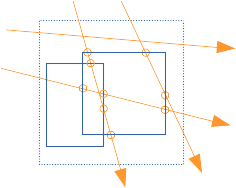
plus intuitivement : on peut se représenter les 2N points d'intersections des N droites avec l'englobant P du père :

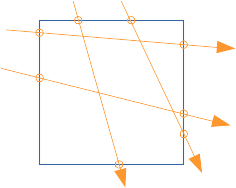
si une autre boite plus petite se trouve dans P, moins de droites et de points d'intersections la touchent : et le rapport des nombres de points d'intersections correspond au nombre de fois ou la petite boite est touchée par les droites.

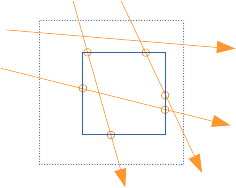
ce résultat est issu des proba, et il faut imaginer qu'en moyenne, sur une infinité de tests avec N droites, on a le bon résultat...

si plusieurs petites boites se trouvent dans P, le rapport des points d'intersections correspond, en moyenne, au nombre de boites touchées par les droites.

et alors ?

on peut utiliser cette relation pour comparer plusieurs répartitions de triangles entre les 2 fils d'un noeud... Pour une répartition, chaque fils est associé à un sous-ensemble de triangles, si on connait aussi le nombre de visites de chaque fils, on peut calculer le nombre de tests d'intersections rayon/triangle... et garder la répartition qui réalisera le moins de tests d'intersections.

exemple : on a T triangles. sans répartition, il faudra tous les tester pour chaque rayon : on calculera T tests rayon/triangle. si on répartit les triangles en 2 sous-ensembles T1 et T2, on peut aussi calculer l'englobant F1 des triangles T1 et l'englobant F2 des triangles T2 et on connait l'englobant P des T triangles.

combien de tests rayon/triangle pour une répartition T1/T2 ?

on peut estimer \( \frac{aire(F1)}{aire(P)}\) et \( \frac{aire(F2)}{aire(P)}\), le nombre de fois ou les fils 1 et 2 seront visités. donc on fera au total \( \frac{aire(F1)}{aire(P)} \times T1 \) tests rayon/triangle lors des visites du fils 1, et \( \frac{aire(F2)}{aire(P)} \times T2 \) tests rayon/triangle pour le fils 2.

Pour les droites visitant les 2 fils, on fera autant de tests rayon/triangle que sans la répartition, par contre dans les autres cas, on fera moins de tests, mais il faudra aussi tester les englobants des 2 fils. La répartition ne sera interessante que si on fait moins de T tests rayon/triangle en moyenne.

les 2 exemples de répartitions utilisées pour construire le BVH reviennent soit à controler le nombre de triangles T1 et T2, soit à "controler" (plus ou moins précisement) les englobants F1 et F2 :

• solution 1 : T1= T/2, T2= T/2, puis on estime les englobants F1 et F2, mais on ne connait pas, a priori leur taille,
• solution 2 : on répartit les triangles dans T1 et T2 en fonction de leur position par rapport au milieu de P, puis on estime F1 et F2 qui correspondent plus ou moins à la moitiée de P : F1= ~P/2, F2= ~P/2, mais on ne connait pas a priori le nombre de triangles associé à chaque fils.

En pratique on pourrait très bien estimer le nombre d'intersections rayon/triangle pour les 2 solutions avant de construire chaque noeud de l'arbre et choisir la meilleure. mais on peut faire mieux que ca !

combien de répartitions ?

maintenant que l'on sait comparer plusieurs répartitions, il ne reste plus qu'à toutes les évaluer, garder la meilleure, et hop, magie, on a le meilleur arbre possible...

comment ça, c'est débile comme solution ? ben, il y a, à peu près, \( 2^T \) manières de répartir T triangles en 2 groupes... ca fait un poil beaucoup... même pour T= 32, comme dans la cornell_box, on a pas du tout envie de les tester, et pour T= 64 on a pas le temps de faire le calcul...

et alors ?

on va limiter le nombre de répartitions de triangles que l'on va tester... on ne regarde que la projection des englobants des triangles triés sur les 3 axes, ce qui ne fait que 3T répartitions à tester. mieux, non ? ben, ça dépend...

De manière générale, on va construitre un arbre binaire avec 1 triangle par feuille, soit T feuilles (par la suite on utilise F= T pour le nombre de feuilles). Un arbre binaire avec F feuilles aura N= F-1 noeuds internes et 2T-1 englobants au total (F englobants pour les feuilles et N englobants pour les noeuds).

On peut estimer combien de noeuds , et combien de feuilles, vont être touchés par des droites uniformes en utilisant les résultats de la section précédente :

\[ \begin{eqnarray*} noeuds &=& \sum_{i=1}^{N}\frac{aire(n_i)}{aire(racine)}\\ feuilles &=& \sum_{i=1}^{F} \frac{aire(f_i)}{aire(racine)}\\ \end{eqnarray*} \]

avec \( \{ n_i \} \) les noeuds internes, et \( \{ f_i \} \) les feuilles.

on sait que pour chaque visite d'un noeud interne, on teste l'intersection du rayon avec les englobants des 2 fils, et pour chaque visite d'une feuille on teste l'intersection du rayon avec \( T_i\) triangles. Si on mesure le temps d'execution d'un test d'intersection rayon/englobant, noté \( C_{box} \) et le temps d'execution d'un test rayon/triangle, noté \( C_{triangle} \), on peut estimer le temps moyen d'intersection d'un rayon avec les englobants et les triangles de l'arbre :

\[ \begin{eqnarray*} C &= & noeuds \times 2C_{box} + feuilles \times C_{triangle}\\ C &= & \sum_{i=1}^{N}\frac{aire(n_i)}{aire(racine)} \times 2C_{box} + \sum_{i=1}^{F} \frac{aire(f_i)}{aire(racine)} \times T_i \times C_{triangle} \end{eqnarray*} \]

et il ne reste plus qu'à minimiser \( C \), le temps d'intersection, ou de manière générale, le cout de l'arbre...

cette formulation a été introduite dans :
”Heuristics for ray tracing using space subdivison” J.D. MacDonald, K.S. Booth, 1989
et cette manière de construire un BVH s'appelle SAH, pour surface area heuristic.

construction de BVH par minimisation du cout / SAH

que peut-on modifier/optimiser dans l'expression du cout d'un arbre ? les feuilles et leurs englobants sont fixés par la géométrie/les triangles. le nombre de noeuds internes est fixé lui aussi (cf arbre binaire...), donc le seul dégré de liberté est la taille des englobants des noeuds internes... et on sait deja qu'il faut qu'ils soient les plus petits possibles pour limiter le nombre de visites / de tests d'intersection des englobants.

glouton ?

construire un arbre de recherche optimal n'est pas simple, mais on peut utiliser une statégie gloutone qui essaye de répartir récursivement les triangles en 2 groupes. L'algorithme démarre avec l'ensemble complet des triangles de la scène, le coupe en 2, puis recommence récursivement sur chaque sous ensemble. chaque étape de l'algorithme permet de construire un noeud et ses 2 fils et s'arrete, en créant une feuille, lorsqu'il ne reste plus qu'un seul triangle. c'est la même stratégie que l'algorithme de répartition dans le lancer de rayons, ça rame ? ou pas ?.

pour chaque noeud, on souhaite trouver une répartition de triangles qui minimise le cout du noeud : c'est à dire

\[ 2C_{box} + \frac{aire(F1)}{aire(P)} \times T1 \times C_{triangle} + \frac{aire(F2)}{aire(P)} \times T2 \times C_{triangle} \]

avec F1 l'englobant des T1 triangles associés au fils 1, et F2, l'englobant des T2 triangles associés au fils 2. autrement dit, pour chaque visite du noeud, on estime le temps nécessaire à tester l'intersection des englobants des 2 fils, et pour chaque visite d'un fils, on estime le temps nécessaire à tester l'intersection avec le sous ensemble correspondant de triangles.

remarque : on obtient bien cette expression avec le cout d'un arbre composé d'un seul noeud (sa racine) et de 2 feuilles.

mais comme vu au dessus, on ne peut pas tester la totalité des répartitions possible de triangles, on va 'juste' en tester un nombre raisonnable.

Une solution classique pour tester un nombre raisonnable de répartitions est de trier les triangles le long de chaque axe et de tester chaque répartition obtenue en balayant les triangles par ordre croissant :

• premier triangle dans le fils 1, les autres dans le fils 2,
• les 2 premiers triangles dans le fils 1, les autres dans le fils 2,
• les 3 premiers triangles dans le fils 1, les autres dans le fils 2,
• etc.
• le dernier triangle dans le fils 2, les autres dans le fils 1,

ce qui nous donne T-1 répartitions possibles par axe. on évalue le cout de chacune et on garde la meilleure, la plus petite, que l'on utilise pour construire les 2 fils et recommencer.

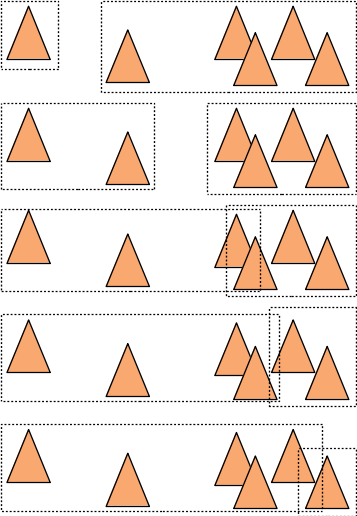
Avec les 6 triangles de l'exemple précédent :

on va évaluer le cout des 5 répartitions que l'on peut construire avec 6 triangles et utiliser celle avec le cout le plus petit pour construire le noeud :

remarque : oui, si le temps estimé est plus grand que \( T \times C_{triangle} \) (tester tous les triangles) la répartition n'est pas très interressante, et c'est probablement le bon moment d'arreter la recursion et de créer une feuille dans l'arbre.

Les détails complets de cet algorithme sont dans :
"Ray Tracing Deformable Scenes using Dynamic Bounding Volume Hierarchies" I. Wald, S. Boulos, P. Shirley, 2007.
(remarque : si vous ne lisez qu'un seul article de lancer de rayons cette année, lisez celui-la, même si certaines optimisations ne sont plus utilisées actuellement)

Cette solution est toujours considérée comme la référence, mais n'est plus vraiment utilisée... pourquoi ? la complexité de l'algorithme est trop importante, cf le master theorm qui permet d'estimer la complexite d'un algorithme récursif. chaque étape de cette méthode nécessite un tri en \(O(n \log n)\) suivi d'un balayage en \( O(n) \), et au total l'algorithme à une complexité trop importante... à l'heure actuelle les scènes sont composées de millions, voir de milliards de triangles et cet algorithme de référence est bien trop long... mais on peut se demander comment obtenir un algorithme avec une complexité plus interessante comme \(O(n \log n)\). La encore le master theorem fournit la réponse, il faut que la complexité de chaque étape soit linéaire, en \( O(n) \)... le tri n'est donc pas possible !

Mais on peut remplacer le tri par un hachage spatial, qui lui est en \( O(n) \). les détails sont dans :
"On fast Construction of SAH-based Bounding Volume Hierarchies" I. Wald, 2007.
(remarque : si vous ne lisez qu'un seul article de construction d'arbre cette année, lisez celui-la...)

La construction des répartitions est un peu différente mais le principe reste le même : on a plusieurs manières de répartir les triangles entre les 2 fils, on évalue le cout de chaque répartition et on utilise la meilleure pour construire le noeud.

Par exemple, avec un histogramme / hachage spatial à 4 cellules :

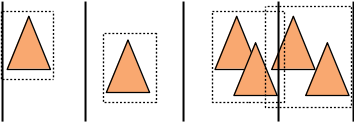
La première étape construit l'histogramme. On utilise le centre de l'englobant de chaque triangle pour décider dans quelle cellule le placer. Il ne reste plus qu'à construire l'englobant des triangles qui occuppent chaque cellule (et oui, l'englobant peut "déborder" de la cellule, comme la 3ieme et la 4ieme de l'exemple).

Ensuite, on évalue le cout des répartitions que l'on peut construire avec les cellules de l'histogramme :

• triangles de la première cellule dans le fils 1, les autres dans le fils 2,
• triangles des 2 premières cellules dans le fils 1, les autres dans le fils 2,
• etc.
• triangles de la dernière cellule dans le fils 2, les autres dans le fils 1.

ce qui donne n-1 répartitions à tester pour un histogramme à n cellules :

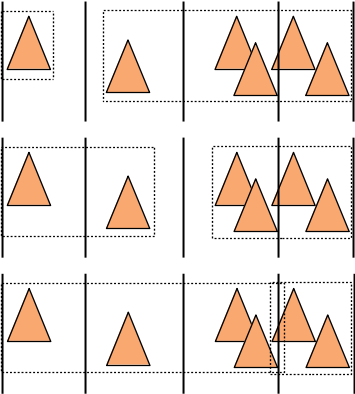
Bien sur, on peut se demander combien de cellules utiliser, après pas mal de tests, 12 ou 16 cellules fonctionnent correctement. Ce qui correspond aussi aux résultats de l'article.

struct Bucket
{
    BBox bounds;
    int n;
    
    Bucket( ) : bounds(EmptyBox()), n(0) {}
};
 
int build_node( const int begin, const int end )
{
    assert(end > begin);
    
    // construire l'englobant des triangles
    BBox bounds= triangle_bounds(begin, end);
    
    if(end - begin <= 2)
    {
        // construire une feuille
        int index= int(nodes.size());
        nodes.push_back( make_leaf(bounds, begin, end) );
        return index;
    }
    
    // construire l'englobant des centres des englobants des triangles pour evaluer les repartitions
    BBox cbounds= centroid_bounds(begin, end);
    
    // compare le cout de la repartition sur chaque axe et garde le meilleur...
    float area= bounds.area();    
    int min_axis= -1;
    int min_index= -1;
    float min_cost= FLT_MAX;
    for(int axis= 0; axis < 3; axis++)
    {
        // hachage spatial, remplace le tri des triangles sur l'axe
        const int BUCKETS_MAX= 16;
        Bucket buckets[BUCKETS_MAX];
        
        // compte le nombre de triangles par cellule de l'histogramme
        for(int i= begin; i < end; i++)
        {
            // 'projette' le centre de l'englobant du triangle dans l'histogramme
            int k= BUCKETS_MAX * (triangles[i].centroid(axis) - cbounds.pmin(axis)) 
                / (cbounds.pmax(axis) - cbounds.pmin(axis));
            if(k <= 0) k= 0;
            if(k >= BUCKETS_MAX) k= BUCKETS_MAX -1;
            // attention aux calculs sur les floats... verifier que k est bien un indice de cellule
 
            buckets[k].bounds.insert(triangles[i].bounds());    // englobant des triangles de la cellule k
            buckets[k].n++;                                     // nombre de triangles de la cellule k
        }
        
        // evalue chaque repartition possible : fils 1 cellules entre 0 et i, le fils 2 recupere les autres...
        // 1|n-1, 2|n-2, 3|n-3 ... n-1|1
        for(int i= 1; i < BUCKETS_MAX-1; i++)
        {
            BBox left= EmptyBox();
            int left_n= 0;
            for(int k= 0; k < i; k++)                           // cellules de 0 à i
            {
                left_n+= buckets[k].n;
                left.insert(buckets[k].bounds);
            }
            assert(left_n > 0);
 
            BBox right= EmptyBox();
            int right_n= 0;
            for(int k= i; k < BUCKETS_MAX; k++)                 // cellules de i a n
            {
                right_n+= buckets[k].n;
                right.insert(buckets[k].bounds);
            }
            assert(right_n > 0);
            
            // evalue le cout de la repartition
            float cost= 2                                       // 2 tests rayon/boite
                + left.area() / area * left_n                   // + visites du fils 1 * triangles du fils 1
                + right.area() / area * right_n;                // + visites du fils 2 * triangles du fils 2 
                
            if(cost < min_cost)                                 // garde la meilleure repartition
            {
                min_cost= cost;
                min_axis= axis;
                min_index= i;
            }
        }
    }
    
    // repartir les triangles 
    int m= begin;
    if(min_axis != -1)
    {
        auto *p= std::partition(triangles.data() + begin, triangles.data() + end, 
            bucket_less(min_index, min_axis, cbounds.pmin(min_axis), cbounds.pmax(min_axis)));
        m= std::distance(triangles.data(), p);
    }
    
    if(m == begin || m == end)  // si la repartition echoue, couper arbitrairement
        m= (begin + end) / 2;
    
    // repartir les triangles et construire les fils du noeud
    int left= build_node(nodes, begin, m);
    int right= build_node(nodes, m, end);
    
    // construire le noeud
    int index= int(nodes.size());
    nodes.push_back( make_node(bounds, left, right) );
    return index;
}
 
// et le predicat pour partitionner les triangles
struct bucket_less
{
    int axis, index;
    float cmin, cmax;
    
    bucket_less( const int _index, const int _axis, const float _cmin, const float _cmax ) 
        : axis(_axis), index(_index), cmin(_cmin), cmax(_cmax) {}
    
    bool operator() ( const Triangle& triangle ) const
    {
        int k= buckets_max * (triangle.centroid(axis) - cmin) / (cmax - cmin);
        return k < index;
    }
};
 
// il manque aussi une fonction membre de BBox pour calculer l'aire d'une boite
float BBox::area( ) const
{
    Vector d(pmin, pmax);
    return 2 * d.x*d.y + 2 * d.x*d.z + 2 * d.y*d.z;
}
 
// et la construction des englobants des centres des englobants des triangles,
// pour une fois le code est plus simple a comprendre que la phrase qui le decrit... 
BBox centroid_bounds( const int begin, const int end )
{
    BBox bounds= EmptyBox();
    for(int i= begin; i < end; i++)
    {
        Point c= triangles[i].bounds().centroid();
        bounds.insert(c);
    }
    
    return bounds;
}

et ça marche ?

on peut évaluer le cout des arbres construit par les solutions précédentes (et les comparer au temps de rendu mesurés...) :

• solution 1 : trier les triangles et répartir chaque moitiée dans un fils, construction BVH 0.6s, rendu 28s, cout 177,
• solution 2 : répartir les triangles dans chaque fils en fonction de leur position dans l'englobant, construction BVH 0.1s, rendu 10s, cout 106,
• solution 2+ : idem solution 2, mais évalue le cout sur chaque axe et utilise la meilleure répartition, construction BVH 0.2s, rendu 8s, cout 112,
• solution 3 : minimisation du SAH par hachage spatial, construction BVH 0.8s, rendu 6s, cout 86.

ainsi que le nombre de noeuds et de feuilles visités :

• solution 1 : rendu 28s, cout 177, noeuds visités 156, feuilles 20
• solution 2 : rendu 10s, cout 106, noeuds visités 86, feuilles 20
• solution 2+ : rendu 8s, cout 116, noeuds visités 96, feuilles 20
• solution 3 : rendu 6s, cout 86, noeuds visités 66, feuilles 20

c'est pas mal, effectivement, évaluer plusieurs répartitions pour construire chaque noeud de l'arbre prend un peu de temps, mais les intersections rayon/arbre sont nettement plus rapides.

autre remarque : le cout ne représente pas exactement le temps d'exécution, par exemple pour les solutions 2 et 2+...

peut mieux faire...

il est quand meme dommage de créer autant de feuilles, non ?? le cout d'un noeud donne une indication : on peut arreter la construction de l'arbre et créer une feuille, lorsque le plus petit cout estimé est plus grand que tester les T triangles. et par construction, s'il y a moins de noeuds et de feuilles, le cout total de l'arbre sera plus petit.

• solution 2+ : noeuds 524533, cout 116, noeuds visités 96, feuilles 20
  vs noeuds 270889, cout 106, noeuds visités 77, feuilles 9
• solution 3 : noeuds 524533, cout 86, noeuds visités 66, feuilles 20
  vs noeuds 262013, cout 77, noeuds visités 53, feuilles 7

le temps d'exécution diminue légèrement mais surtout l'arbre contient beaucoup moins de noeuds internes et sera plus compact en mémoire. par contre, les feuilles contiennent plus de triangles qu'il faudra tester.

parcours efficace

Tous les algorithmes de parcours visitent tous les noeuds et toutes les feuilles touchés par le rayon. Par contre, certains sont plus rapides que d'autres... ils ne parcourent que la partie strictement nécessaire de l'arbre pour trouver la feuille contenant le triangle touché par le rayon.

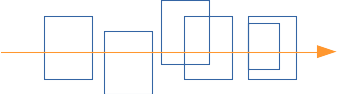
Si l'on souhaite trouver rapidement l'intersection la plus proche de l'origine du rayon, il est necessaire de parcourir les feuilles dans le bon ordre : par position croissante le long du rayon. c'est direct lorsque les englobants sont séparés, mais moins évident lorsqu'ils se chevauchent comme dans les BVH :

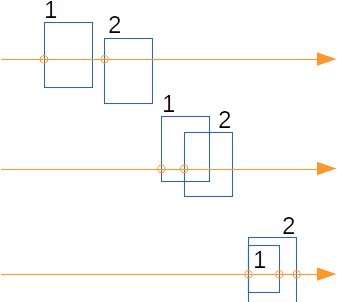
et le problème est de choisir dans quel ordre visiter les fils des noeuds internes pour parcourir les feuilles le long du rayon en s'éloignant de l'origine du rayon. Les différents cas sont représentés sur le schéma précédent. Lorsque les englobants des fils sont séparés, pas de problème, il suffit de comparer la position des points d'entrés dans les englobants. Lorsqu'ils se chevauchent partiellement, la comparaison des points d'entrés fournit également la bonne réponse. Reste le dernier cas, les points d'entrée sont confondus, et il suffit de comparer les points de sorties.

On peut résumer le choix de l'ordre de visite des fils :

visit( node, ray )
{
    { bool left, float left_tmin, float left_tmax } = left_node.bounds.intersect(ray);
    { bool right, float right_tmin, float right_tmax } = right_node.bounds.intersect(ray);
 
    if(left && right)                       // les 2 fils sont touches par le rayon
    {
        if(left_tmin < right_tmin)          // parcours de gauche a droite
        {
            // les points d'entree sont differents
            visit(left_node, ray);
            visit(right_node, ray);
        }
        else if(left_tmin == right_tmim && left_tmax < right_tmax)
        {
            // si les points d'entree sont egaux, comparer les points de sorties
            visit(left_node, ray);
            visit(right_node, ray);
        }
        else                                // dans les autres cas, parcours de droite a gauche
        {                                   
            visit(right_node, ray);
            visit(left_node, ray);
        }
    }
    else if(left)                           // uniquement le fils gauche
        visit(left_node, ray);
    else if(right)                          // uniquement le fils droit
        visit(right_node, ray);
}

En pratique, il est plus simple (et plus robuste numériquement) de comparer la position du milieu des intersections avec les englobants :

visit( node, ray )
{
    { bool left, float left_tmin, float left_tmax } = left_node.bounds.intersect(ray);
    { bool right, float right_tmin, float right_tmax } = right_node.bounds.intersect(ray);
 
    if(left && right)                       // les 2 fils sont touches par le rayon
    {
        float left_centroid= (left_tmin + left_tmax) / 2;
        float right_centroid= (right_tmin, right_tmax) / 2;
        if(left_centroid < right_centroid)  // parcours de gauche a droite
        {
            visit(left_node, ray);
            visit(right_node, ray);
        }
        else                                // parcours de droite a gauche
        {                       
            visit(right_node, ray);
            visit(left_node, ray);
        }
    }
    else if(left)                           // uniquement le fils gauche
        visit(left_node, ray);
    else if(right)                          // uniquement le fils droit
        visit(right_node, ray);
}

et alors ?

sur le musée, 1500000 triangles

• parcours classique, 4.5s, cf le lancer de rayons, ça rame ? ou pas ?
• parcours ordonné, 2.5s

pas mal, pour quelques lignes de code...

peut mieux faire...

Le parcours présenté est récursif et on a supposé que le prochain noeud parcouru était un des fils du noeud, mais ce choix n'est pas optimal, il ne garanti pas de visiter les feuilles dans l'ordre croissant le long du rayon...

que se passe-t-il dans ce cas :

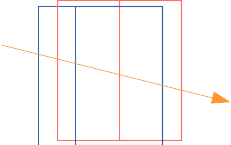
le parcours récursif commence par visiter le noeud bleu et ses fils, puis visite le noeud rouge et ses fils, alors que le bon ordre serait plutot :

• fils gauche bleu,
• fils gauche rouge,
• fils droit bleu,
• fils droit rouge,

c'est à dire l'ordre global des fils... le prochain noeud à visiter n'est pas un des fils du noeud, mais le plus proche de l'origine du rayon, parmi ceux qui reste à visiter...

on peut construire ce parcours en conservant une file de noeuds à visiter, au lieu d'une pile. mais dans la plupart des cas, extraire le prochain noeud à visiter en parcourant la file est trop long, et le gain sur le nombre de noeuds visités ne compense pas le temps de mise à jour de la file.

les détails sont dans :
"Ray tracing complex scenes" T.L. Kay, J.T. Kajiya, 1986

ça marche ? ou pas (trop) ?

il existe de nombreuses manières de construire des BVH, et certaines fonctionnent mieux que d'autres. Il reste tout de même une question : comment estimer correctement le temps moyen d'intersection d'un rayon. l'heuristique présentée dans les sections précédentes peut etre assez éloignée de la réalité. par exemple, les solutions 2 et 2+, le temps de parcours mesuré ne correspond pas à l'estimation... pourquoi ? le modèle de cout suppose que les rayons sont distribués uniformement, et ce n'est pas le cas pour tous les rayons, ceux qui viennent de la camera, par exemple, ni pour ceux qui testent les ombres et les pénombres d'une source de lumière. Autre limitation, l'estimation du nombre de visite de chaque noeud est exacte pour des droites uniformes, mais il y a plusieurs rayons sur chaque droite qui traverse un noeud...

”On Quality Metrics of Bounding Volume Hierarchies” T. Aila, T. Karras, S. Laine, 2013
compare les différentes solutions et vérifie que l'on peut améliorer la qualité de l'estimation en tenant compte de l'aire des triangles/de la géométrie présente dans l'englobant d'un noeud.

”Cost prediction for ray shooting in octrees” B. Aronov, H. Brönnimann, A.Y. Chang, Y.J. Chiang, 2005
introduit une formulation différente du cout d'un noeud et d'un arbre, qui détermine le nombre moyen de rayons qui visitent chaque noeud (et cette estimation utilise l'aire des triangles présents dans l'englobant du noeud).

le principe de cette estimation est relativement intuitif : si une droite traverse l'englobant d'un noeud sans toucher de géométrie (sans créer un point d'intersection), on considère qu'elle ne porte qu'un seul rayon. par contre, si une droite touche un triangle, elle génère 2 rayons, si elle touche 2 triangles, elle génère 3 rayons, etc. Si on peut estimer ou connaitre le nombre moyen d'intersections pour un ensemble uniforme de droites, on peut estimer le nombre de rayons...

la solution est très simple, en utilisant une fois de plus la même propriété : la somme des aires des triangles divisée par l'aire de l'englobant... la définition se trouve aussi dans :
"Some Integral Geometry Tools to Estimate the Complexity of 3D Scenes", F. Cazals, M. Sbert, 1997.

on peut estimer le nombre de visites d'un noeud \( n \) avec le nombre de droites (passant par le noeud) multiplié par le nombre de rayons par droite, en sommant l'aire des (bouts de) triangles se trouvant dans l'englobant du noeud :

\[ aire(n) \left[ 1 + \frac{\sum_k 2 \times aire(triangle_k \cap n)}{aire(n)} \right] = aire(n) + \sum_k 2 \times aire(triangle_k \cap n) \]

et re-écrire le cout d'un arbre, en normalisant par R le nombre de rayons dans toute la scène (nombre de rayons de la racine) :

\[ \begin{eqnarray*} C & = & \sum_{i=1}^{N} noeud_i \times 2C_{box} + \sum_{i=1}^F feuille_i \times T_i \times C_{triangle}\\ noeud_i & = & \frac{1}{R} \left[ aire(n_i) + \sum_k 2 \times aire(t_k \cap n_i) \right]\\ feuille_i & = & \frac{1}{R} \left[ aire(f_i) + \sum_k 2 \times aire(t_k \cap f_i) \right]\\ R & = & aire(racine) + \sum_k 2 \times aire(t_k) \end{eqnarray*} \]

par contre, pour faire cette estimation pendant la construction d'un bvh, il va falloir déterminer l'aire de la géométrie présente dans l'englobant du noeud, et donc calculer l'aire de l'intersection des triangles \( \sum_k 2 \times aire(t_k)\) avec son englobant. c'est numériquement assez pénible à faire (de manière robuste), et aussi très long à calculer...

comment ça, les arbres équilibrés ne sont pas efficaces ?

Lorsque l'on compare les solutions 1 et 2 :

• solution 1 : trier les triangles et répartir chaque moitiée dans un fils, construction BVH 0.6s, rendu 28s, cout 177,
• solution 2 : répartir les triangles dans chaque fils en fonction de leur position dans l'englobant, construction BVH 0.1s, rendu 10s, cout 106,

le résultat est quand même surprenant... mais il ne faut pas confondre la structure de l'arbre (la hauteur du fils gauche et du fils droit) avec la méthode de répartition des triangles. Dans les arbres binaires de recherche classiques (sur des valeurs simples), répartir le même nombre de valeurs dans les 2 fils produit un arbre efficace à parcourir. pourquoi ? le nombre de visites des fils est equilibré, il y a autant de recherches qui visitent chaque fils (lorsque les recherches sont distribuées uniformement sur les valeurs organisées dans l'arbre), et chaque fils n'est visité que par la moitié des recherches. Pour obtenir le même comportement avec les BVH, il faut minimiser et équilibrer le nombre de visites des fils. Les différentes méthodes de construction minimisent le nombre de visites, mais l'équilibre n'est pas explicitement recherché. Il n'est pas toujours possible de garantir qu'en moyenne un seul fils est visité : il faudrait que \( \frac{aire(F1) + aire(F2)}{aire(P)} <= 1 \) pour chaque noeud de l'arbre.

mais bien sur, on peut essayer de restructurer le bvh pour équilibrer sa structure (hauteur des 2 fils équivalente) :
"Tree Rotations for Improving Bounding Volume Hierarchies" A. Kensler, 2008 et
"Fast Insertion-Based Optimization of Bounding Volume Hierarchies" J. Bittner, M. Hapala, V. Havran, 2013

remarque : ces 2 méthodes esayent aussi de trouver un minimum global du cout de l'arbre, puisque la construction gloutonne / la répartition utilisée dans les sections précédentes est garantie de trouver un minimum local. essayer de trouver un arbre avec un cout plus faible est aussi interressant... mais il est assez difficile d'équilibrer le temps d'optimisation et les performances du parcours de l'arbre, à moins de lancer des milliards de rayons...

pour les curieux : comment construire un arbre binaire de recherche optimal, en temps raisonnable ?
"Nearly Optimal Binary Search Trees" K. Mehlhorn, 1975

que peut-on faire (de plus) pour minimiser le nombre moyen de fils visités ?

Pour être efficace, chaque noeud devrait vérifier : \( \frac{aire(F1) + aire(F2)}{aire(P)} <= 1 \) (un seul fils visité en moyenne), lorsque ce n'est pas le cas, il est possible d'utiliser plus de fils pour mieux répartir les triangles, l'idée est présentée dans cet article :
"Shallow Bounding Volume Hierarchies for Fast SIMD Ray Tracing ofIncoherent Rays" H. Dammertz, J. Hanika, A. Keller, 2008

ou de découper les triangles génants :
"Spatial splits in bounding volume hierarchies" M. Stich, H. Friedrich, A. Dietrich, 2009