gKit2 light
introduction api 3d, openGL et pipeline graphique

introduction : une api 3d ? c'est quoi ?

facile, c'est un ensemble de fonctions permettant de paramétrer un pipeline graphique pour dessiner des objets...

un pipeline graphique ? c'est quoi ?

c'est l'ensemble de traitements qui permet de dessiner des objets.

et openGL ?

c'est une api 3d permettant d'utiliser une carte graphique pour dessiner des objets.

et alors ?

une api 3d permet de configurer et de paramétrer les différentes étapes d'un pipeline graphique. pour comprendre comment utiliser openGL, il faut avoir quelques idées sur le fonctionnement de ces étapes...

exemple : pour dessiner un point, il faut connaitre ses coordonnées, les convertir en position dans l'image et choisir une couleur pour le pixel. si on voulait construire un pipeline pour dessiner des points, il faudrait :

mais il faut aussi définir comment passer des coordonnées du point (entre -1 et 1) aux coordonnées du pixel dans l'image (entre largeur et hauteur).

pour dessiner un triangle, un pipeline à besoin de ces informations pour les 3 sommets du triangle. mais il y a des choix à faire : par exemple, si les 3 sommets n'ont pas la même couleur, laquelle choisir ?

en gros, le pipeline peut proposer plusieurs solutions standards, mais la solution la plus souple est d'écrire une fonction qui fait exactement ce que l'on veut et de la "donner" au pipeline pour qu'il l'utilise.

pour dessiner plusieurs triangles, il faut "donner" au pipeline les coordonnées et les couleurs des sommets de chaque triangle. que se passe-t-il lorsque plusieurs triangles se dessinent sur le même pixel de l'image ?

en résumé, les fonctions de l'api openGL permettent de :

et à chaque fois, les mêmes étapes se repètent, créer un objet (un buffer par exemple, pour stocker les informations sur les sommets) et de configurer le pipeline pour utiliser les informations/paramètres qu'il contient pour dessiner des triangles, des points, ou des droites.

pipeline graphique openGL

le pipeline openGL est découpé en 2 parties :

ces 2 parties sont à moitié programmable, avec des shaders, et à moitié configurable, il faut choisir quelle solution standard utiliser. par exemple, il faut choisir quel triangle donne sa couleur à chaque pixel de l'image, soit en fonction de sa profondeur (le plus proche ou le plus loin), soit en fonction de l'ordre d'affichage. autre option disponible, on peut choisir de dessiner tout le triangle (son intérieur et son bord), ou uniquement son bord, voire uniquement ses sommets.

pipeline géométrique

le role de la première partie est de préparer le dessin des triangles, et son principal travail est de transformer les positions des sommets pour déterminer sur quel pixel de l'image ils se projettent.

pourquoi faut-il transformer les positions des sommets ?

quand on crée un objet, on le dessine tout seul, avec un logiciel comme blender, par exemple, ou on le construit en calculant la position de chacun de ses sommets.

ensuite ces objets, crées séparement, sont disposés dans une scène, il faut les placer, les orienter, ajuster leur taille, etc. pour dessiner ces objets, il faut choisir un point de vue, une camera, qui est aussi placée et orientée dans la scène. et l'information nécessaire pour dessiner un triangle est de savoir sur quels pixels le dessiner, quelque soit la position de la camera. si la camera bouge, les triangles doivent aussi se déplacer dans l'image pour recréer une vue correcte de la scène.

au final, les sommets existent dans plusieurs repères :

le même sommet à donc 5 ou 6 coordonnées différentes (selon qu'il est visible ou pas, un sommet non visible dans l'image n'a pas de coordonnées image).

en résumé, cette première partie du pipeline doit déterminer où se trouve chaque triangle par rapport à la caméra. si un triangle est devant caméra, il sera visible dans l'image, et les coordonnées de ses sommets dans le repère image permettent de le dessiner.

comment ça marche ?

pour placer un triangle dans la scène, on modifie les coordonnées de ses sommets, que l'on connait dans son repère de création. la transformation dans ce cas, est une translation. on ajoute un déplacement, un vecteur, à chaque point. (cf wikipedia)

si l'on veut faire tourner / réorienter un triangle autour d'un axe, ou d'un vecteur, on peut calculer ses nouvelles coordonnées, avec le sinus et le cosinus de l'angle de la rotation. (cf wikipedia)

le changement, le passage d'un repère au suivant peut se représenter à chaque fois de manière assez directe avec une matrice (qui n'est au final, qu'une notation compacte pour un calcul un peu long à écrire avec les 3 coordonnées de chaque sommet). le cas des translations et des projections est un peu à part et nécessite des matrices avec une ligne et une colonne de plus. (cf wikipedia)

mais au final, le passage d'un repère au suivant se représente avec une matrice 4x4 :

tous les pipelines 3d utilisent ces matrices, même si ce n'est pas toujours intuitif à manipuler. par contre, ces matrices ont des propriétés très interressantes : on peut multiplier plusieurs matrices pour sauter plusieurs changements de repères, ce qui permet de faire des calculs plus rapides, on peut inverser une matrice pour obtenir le passage dans l'autre sens, ce qui permet, par exemple, de faire du lancer de rayons, on peut facilement construire des objets articulés et les animer, ou faire bouger des objets les uns par rapport aux autres... et tout ca serait beaucoup plus difficile ou limité sans utiliser de matrices.

et openGL ?

openGL à besoin de connaitre les coordonnées des sommets des triangles dans le repère projectif homogène de la camera pour pouvoir ensuite dessiner les triangles, et comme on écrit une fonction qui fait le calcul, on est libre d'utiliser des matrices, ou pas... il faut "juste" l'expliquer à openGL, et écrire le vertex shader responsable de cette partie du pipeline.

si on souhaite écrire une fonction en C/C++ qui déplace un sommet, on aura quelque chose comme ca :

struct Point
{
float x, y, z, w;
};
Point transform( const Point position, const float dx, const float dy, const float dz )
{
Point r;
r.x= position.x + dx;
r.y= position.y + dy;
r.z= position.z + dz;
r.w= 1;
return r;
}
Point
representation d'un point 3d.
Definition: vec.h:21

pour simplifier les calculs, on choisit des sommets qui sont deja placés devant la camera, et par convention, leurs coordonnées doivent être entre -1 et 1 sur x, y, et z, pour être visible. la 4ieme coordonnée est 1 pour un point.

(rappel : vu que les transformations sont représentées par des matrices à 4 lignes de 4 colonnes, un point ou un vecteur à forcement 4 coordonnées : x, y, z et w, le poids homogène)

cette fonction ne transforme qu'un seul sommet, il faut donc l'utiliser 3 fois pour déplacer un triangle. openGL impose une solution particulière : par defaut, il se contente de numéroter les sommets, le shader ne prend en entrée qu'un seul paramètre, l'indice du sommet à tansformer. la fonction s'appelle main et le résultat doit être écrit dans une variable globale.

le shader ressemble plutot à ça :

struct Point
{
float x, y, z, w;
};
// variables definies par l'application
const float dx= ... ;
const float dy= ... ;
const float dz= ... ;
const int gl_VertexID = ... ; // valeur donnée par openGL
Point gl_Position; // stockage du résultat, utilise par la suite du pipeline
void main( )
{
const Point positions[3] = { { ... }, { ... }, { ... } };
Point r;
r.x= positions[gl_VertexID].x + dx;
r.y= positions[gl_VertexID].y + dy;
r.z= positions[gl_VertexID].z + dz;
r.w= 1;
gl_Position= r;
}

cette fonction est appellée pour déplacer chaque sommet des triangles que l'on dessine, et gl_VertexID change de valeur à chaque fois. en gros, le pipeline openGL utilise le vertex shader de cette manière :

/*
une carte graphique fait quelque chose d'équivalent (mais en parallèle et avec du matériel spécialisé),
une fois que les 3 sommets d'un triangle sont transformés, on peut dessiner le triangle.
*/
Point vertex_shader( const int vertex_id )
{
// definit les variables globales maniplees par le vertex shader
int gl_VertexID= vertex_id;
Point gl_Position;
// execute la fonction main() du vertex shader
{ ... }
// renvoie la position transformee
return gl_Position;
}
void draw( const int count )
{
for(int i= 0; i +2 < count; i= i +3)
{
// transforme les 3 sommets du triangle en utilisant le vertex shader
Point a= vertex_shader(i);
Point b= vertex_shader(i +1);
Point c= vertex_shader(i +2);
// dessiner un triangle par triplet de sommets...
draw_triangle(a, b, c);
}
}

le plus simple est de le tester.

compilez shader_kit.cpp et jouez un peu avec le shader intro1.glsl

./bin/shader_kit tutos/intro1.glsl

ouvrez tutos/intro1.glsl avec un éditeur, faites des modifications, réactivez la fenêtre de shader_kit et appuyez sur R pour recharger le shader...

remarque: shader_kit n'affiche qu'un seul triangle de cette manière...

et avec plusieurs triangles ?

le vertex shader est presque le même, mais le tableau de sommets est global, et sa déclaration est un peu particulière, et c'est l'application qui le remplit, pas le shader.

// valeurs definies par l'application
uniform vec3 positions[12];
const float dx= ... ;
const float dy= ... ;
const float dz= ... ;
void main( )
{
Point r;
r.x= positions[gl_VertexID].x + dx;
r.y= positions[gl_VertexID].y + dy;
r.z= positions[gl_VertexID].z + dz;
r.w= 1;
gl_Position= r;
}
vec3
vecteur generique, utilitaire.
Definition: vec.h:146

le mot-clé uniform, indique que le tableau positions ne change pas pendant l'exécution du pipeline. c'est bien ce que l'on veut, du point de vue du vertex shader le tableau est une constante et le shader doit transformer tous les sommets du tableau pour pouvoir dessiner les triangles. par contre, l'application peut changer le contenu du tableau pour afficher un autre ensemble de triangles.

la différence principale avec la première solution : l'application remplit le tableau positions, fournit le shader et demande à openGL de dessiner 12 sommets, soit 4 triangles. c'est ce qu'il faut retenir : un shader, et le pipeline graphique en général, fonctionne avec les données et paramètres fourni par l'application, ils sont dépendents l'un de l'autre.

c'est la solution la plus directe pour dessiner quelques triangles, mais elle est limitée. les variables et tableaux déclarés comme uniform ne peuvent pas occupper plus de 64Ko (les 4 floats de chaque sommet, occuppent 16 octets, donc on peut dessiner 64000 / 16 / 3 = à peu près 1000 triangles).

la solution "normale" est un peu plus longue à mettre en place, mais fonctionne exactement de la même manière.

si vous êtes pressés, vous pouvez consulter les autres tutos pour écrire une première application openGL. mais il est conseillé de jeter un oeil à la 2ieme partie du pipeline...

raccourcis : pour écrire une première application openGL qui utilise les 2 premières solutions :

pipeline pixels

le role de la deuxième partie du pipeline est de dessiner les triangles en connaissant les coordonnées des sommets dans le repère projectif homogène de la caméra. et ces coordonnées sont calculées par la première partie du pipeline.

comment ça marche ?

une fois que les vertex shaders ont été exécutés, le pipeline connait les coordonnées des sommets des triangles dans le repère projectif homogene. mais il reste un test de visibilité à faire, pour déterminer si le triangle est, au moins, en partie visible, ainsi qu'un dernier changement de repère, le passage vers le repere projectif reel et, enfin, vers le repère image.

tous les sommets ont des coordonnées dans le repère projectif, mais, par convention, seuls ceux qui se trouvent dans le cube [-1 1] sur x, y, et z correspondent à des pixels de l'image :

les points homogenes wx, wy, wz, sont donc visibles si :

rappel : on peut retrouver le point réel p = (x, y, z, 1) associé à un point homogène h = (wx, wy, wz, w) en divisant par w, le poids homogene : p = h / h.w.

le premier traitement réalisé est donc ce test de visibilité, suivi, ou pas, de la dernière transformation vers le repère image, et enfin du test qui détermine quels pixels permettent de dessiner le triangle.

on peut écrire le test de visibilité d'un sommet comme ça :

bool visible( const Point p )
{
if(p.x < -p.w || p.x > p.w) return false; // trop à droite, ou à gauche
if(p.y < -p.w || p.y > p.w) return false; // trop haut, ou trop bas
if(p.z < -p.w || p.z > p.w) return false; // trop loin ou derrière
// le sommet reel est bien dans le cube -1 1, il est visible par la camera
return true;
}

si les sommets du triangle ne sont pas tous les 3 visibles, il faudra découper le triangle pour trouver quelle partie est visible. sinon, les coordonnées sont transformées d'abord dans le repere projectif réel, puis en position de pixels dans l'image, et le fragment shader, la fonction responsable de donner une couleur au pixel est exécutée, puis la couleur est écrite dans l'image.

/*
une carte graphique fait quelque chose d'équivalent (mais en parallèle et avec du matériel spécialisé).
*/
struct Image { ... };
Image image = { ... }; // image resultat
int width= ...; // largeur de l'image
int height= ...; // hauteur de l'image
struct Fragment { float x, y; }; // representation d'un fragment
struct Color { float r, g, b; }; // representation d'une couleur
void draw_triangle( const Point a, const Point b, const Point c )
{
if(!visible(a) || !visible(b) || !visible(c))
// le triangle est en partie non visible, il faudra le decouper et ne dessiner que la partie visible
return; // todo
// passage dans le repere projectif reel
a= a / a.w;
b= b / b.w;
c= c / c.w;
// passage dans le repère image, de [-1 1]x[-1 1] vers [0 width]x[0 height]
Point pa= (a + 1) * Point(with, height, 1) / 2;
Point pb= (b + 1) * Point(with, height, 1) / 2;
Point pc= (c + 1) * Point(with, height, 1) / 2;
// dessiner le triangle, parcourir tous les pixels de l'image...
// todo : comment eviter de tous les parcourir ?
for(int y= 0; y < height; y++)
for(int x= 0; x < width; x++)
{
// verifier que le pixel x, y fait partie du triangle...
if(inside(x, y, pa, pb, pc))
{
// executer le fragment shader pour connaitre la couleur du pixel
Fragment gl_FragCoord; // position du fragment
gl_FragCoord.x= x;
gl_FragCoord.y= y;
Color gl_FragColor; // couleur du fragment
gl_FragColor.r= 0;
gl_FragColor.g= 0;
gl_FragColor.b= 0;
// execute la fonction main() du fragment shader
{ ... }
// renvoie la couleur du fragment
// ecrit la couleur dans l'image
image(x, y)= gl_FragColor;
}
}
}
Image
representation d'une image.
Definition: image.h:21
Color
representation d'une couleur (rgba) transparente ou opaque.
Definition: color.h:14

le fragment shader utilise aussi une convention particulière, la position du pixel est disponible dans une variable globale, gl_FragCoord, la couleur du pixel doit être aussi écrite dans une variable globale, gl_FragColor.

fragment : par définition, un fragment est la partie du triangle qui se projette sur un pixel.

le shader le plus simple donne une couleur constante à chaque pixel du triangle :

const Fragment gl_FragCoord= ... ; // valeur donnée par openGL
Color gl_FragColor; // stockage du résultat, utilise par la suite du pipeline
void main( )
{
gl_FragColor= Color(1, 1, 1); // le pixel sera blanc...
}
le triangle et la grille de pixels à tester...

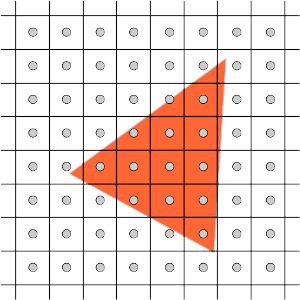
la fonction qui permet vraiment de dessiner le triangle, en testant l'inclusion d'un pixel x, y dans le triangle a, b, c, appelée inside( ), est plus interressante, et c'est un bon exercice...

si openGL ne dessinait qu'un seul triangle de couleur constante, la présentation serait terminée. il y a donc quelques détails supplémentaires...

et avec plusieurs triangles ?

comme évoqué dans l'introduction, plusieurs triangles peuvent se dessiner sur le même pixel. dans ce cas, il faut choisir quelle couleur conserver. une option nécessaire pour obtenir une image cohérente de la scène est de garder la couleur du triangle le plus proche de la camera. si les objets représentés par les triangles sont opaques, c'est la bonne solution...

le pipeline calcule donc une autre information pour chaque fragment : la distance jusqu'à la camera et la conserve pour chaque pixel dans une autre image, le zbuffer.

contrairement à l'intuition, le repère image n'est pas un carre en 2d. la profondeur d'un sommet, sa coordonnée z, est connue, et il suffit de garder le triangle avec le plus petit z, pour chaque pixel de l'image. le repère image est donc un cube en 3d, de dimensions [0 largeur]x[0 hauteur]x[0 1], la profondeur est normalisée entre 0 et 1. la camera n'observe qu'une région de la scène, les triangles trop proches, ainsi que ceux qui sont trop loin, ne sont pas dessinés. ces paramètres sont fournis lors de la construction de la transformation projection. cf les paramètres znear et zfar de Perspective( ).

il y a quand même un problème à régler, le pipeline connait les coordonnées des sommets de chaque triangle, mais il faut calculer les coordonnées de chaque fragment, c'est à dire la coordonnée z pour chaque pixel x, y occuppé par le triangle dans l'image.

une solution est d'interpoler la valeur z pour tous les pixels du triangle. comment ?

la fonction inside( ), qui permet de savoir si un pixel x, y appartient à un triangle a, b, c, fournit quasiment la réponse.

l'idée du test réalisé par inside( ) est de vérifier que le pixel x, y est du "bon" coté des 3 arêtes du triangle.

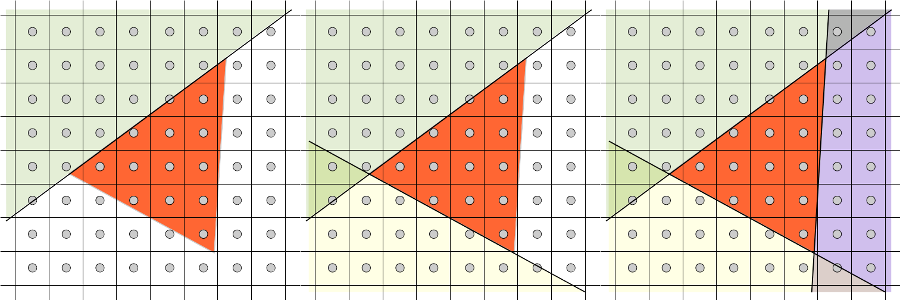
les 3 arêtes à tester, pour chaque pixel...

ce test revient à calculer l'aire signée (algébrique) des 3 triangles formés par le pixel p, et les 3 arêtes ab, bc, et ca (cf Modern triangles / section Modern triangles). si les aires des triangles pab, pbc et pca ont le même signe, le pixel p est à l'intérieur du triangle.

les 2 triangles (verts) ont des aires de signes opposés, à gauche le pixel est à intérieur, à droite, le pixel est à l'extérieur.

dans l'exemple ci dessus, partie gauche, l'aire du triangle vert sera positive si les sommets du triangle abc sont dans le sens trigo et négative dans l'autre cas. on a aire(p, a, b) > 0 (les 3 sommets sont dans le sens trigo) et à droite aire(p, a, b) < 0 (les 3 sommets sont dans le sens horaire).

si le triangle abc est décrit dans l'autre sens, le sens horaire, l'aire change de signe. il est donc très important de décrire les sommets des triangles à dessiner en respectant une orientation et de donner cette information au pipeline pour qu'il prenne les bonnes décisions.

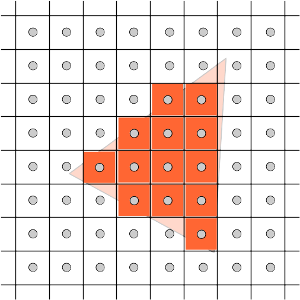
en résumé, si le pixel p fait parti du triangle, on connait l'aire des 3 sous-triangles pab, pbc et pca, et, en plus, on sait, par construction, que la somme de ces 3 aires est égale à celle du triangle a, b, c. ce sont exactement les coordonnées barycentriques du pixel p dans le triangle, et on peut utiliser ces coordonnées pour interpoler la coordonnée z pour le pixel x, y en ne connaissant que les coordonnées des sommets. (cf wikipedia)

résultat: les pixels à l'intérieur du triangle...

au final, dessiner un triangle ressemble plutot à ça :

struct Image { ... };
Image image= { ... }; // image resultat
Image zbuffer= { ... }; // image resultat
int width= ...; // largeur de l'image
int height= ...; // hauteur de l'image
struct Fragment { float x, y, z; }; // representation d'un fragment
struct Color { float r, g, b; }; // representation d'une couleur
void draw_triangle( const Point a, const Point b, const Point c )
{
if(!visible(a) || !visible(b) || !visible(c))
// le triangle est en partie non visible, il faudra le decouper et ne dessiner que la partie visible
return; // todo
// passage dans le repere projectif reel
a= a / a.w;
b= b / b.w;
c= c / c.w;
// passage dans le repère image, de [-1 1]x[-1 1]x[-1 1] vers [0 width]x[0 height]x[0 1]
Point pa= (a + 1) * Point(with, height, 1) / 2;
Point pb= (b + 1) * Point(with, height, 1) / 2;
Point pc= (c + 1) * Point(with, height, 1) / 2;
// dessiner le triangle
for(int y= 0; y < height; y++)
for(int x= 0; x < width; x++)
{
// verifier que le pixel x, y fait partie du triangle...
if(inside(x, y, pa, pb, pc))
{
// executer le fragment shader pour connaitre la couleur du pixel
Fragment gl_FragCoord; // position du fragment
gl_FragCoord.x= x;
gl_FragCoord.y= y;
// interpoler la profondeur du fragment
gl_FragCoord.z= fragment_depth(x, y, pa, pb, pc);
Color gl_FragColor; // couleur du fragment
gl_FragColor.r= 0;
gl_FragColor.g= 0;
gl_FragColor.b= 0;
// execute la fonction main() du fragment shader
{ ... }
// ecrit la couleur dans l'image, si le fragment est plus proche == test de profondeur
if(gl_FragCoord.z < zbuffer(x, y))
{
image(x, y)= gl_FragColor;
zbuffer(x, y)= gl_FragCoord.z;
}
}
}
}

remarque : un code complet et fonctionnel est disponible dans mini pipeline graphique.

implication directe pour l'application, il plutôt important d'initialiser correctement les valeurs du zbuffer avant de dessiner des triangles, sinon le test de profondeur ne conservera pas le bon triangle pour chaque pixel.

quelle est la profondeur max d'un fragment visible ?

c'est ... 1, la coordonnée z d'un sommet visible est comprise entre -1 et 1 dans le repère projectif, et est ensuite normalisée entre 0 et 1 dans le repère image.

une autre conséquence directe de cette interpolation : on peut interpoler n'importe quelle valeur définie sur les sommets du triangle, comme des couleurs, des normales, des coordonnées de textures, etc. ou même calculer une valeur dans le vertex shader et la transmettre au fragment shader.

le pipeline pourrait interpoler automatiquement toutes les informations définies par sommet du triangle et les donner au fragment shader, mais cette solution n'est pas assez souple. par exemple, on peut tres bien calculer les coordonnées de texture d'un sommet sans quelles soient fournies par l'application.

il faut donc un "mécanisme" plus souple : les shaders peuvent déclarer un nouveau type de variable, des varyings qui sont calculés par un shader et récupérés par le shader suivant dans le pipeline. (remarque : cet exemple n'utilise que des vertex et des fragment shaders, mais il y a 5 types de shaders dans le pipeline graphique openGL...)

ces variables sont donc déclarées en sortie du vertex shader et en entrée du fragment shader, et sont bien sur interpolées par le pipeline.

// vertex shader
out vec3 texcoord; // declaration d'une sortie optionnelle, un varying, mot clé: out
uniform vec3 positions[12];
uniform vec3 deplacement;
void main()
{
gl_Position= positions[gl_VertexID] + deplacement; // sortie obligatoire du vertex shader
texcoord= positions[gl_VertexID]; // varying, sortie "optionnelle" du vertex shader, a déclarer avec le mot clé: out
}
// fragment shader
in vec3 texcoord; // declaration d'une entrée optionnelle, un varying, mot clé: in,
// doit avoir le même nom et le même type que la sortie déclarée dans le vertex shader
void main( )
{
vec3 color= vec3(0, 0, 0);
// calculer la couleur du fragment en fonction de texcoord
// construit une grille dans le repere local de l'objet, et donne une couleur en fonction de la distance à la cellule la plus proche
// texcoord contient la position du fragment du triangle visible pour le pixel, et est interpolé par le pipeline
vec3 p= texcoord * 8;
float d= length( p - (floor(p) + 0.5));
if(d > 1) d= 0;
color= vec3(d*0.8*2, d*0.4*2, 0);
glFragColor= color;
}
length
float length(const Vector &v)
renvoie la longueur d'un vecteur.
Definition: vec.cpp:142

résumé

pour résumer, voila à quoi ressemble le pipeline openGL :

certaines étapes sont programmables, ce sont les shaders, et les autres sont paramétrables :

Et voici le même schéma du pipeline, mais annoté avec les fonctions openGL qui permettent de le paramétrer :

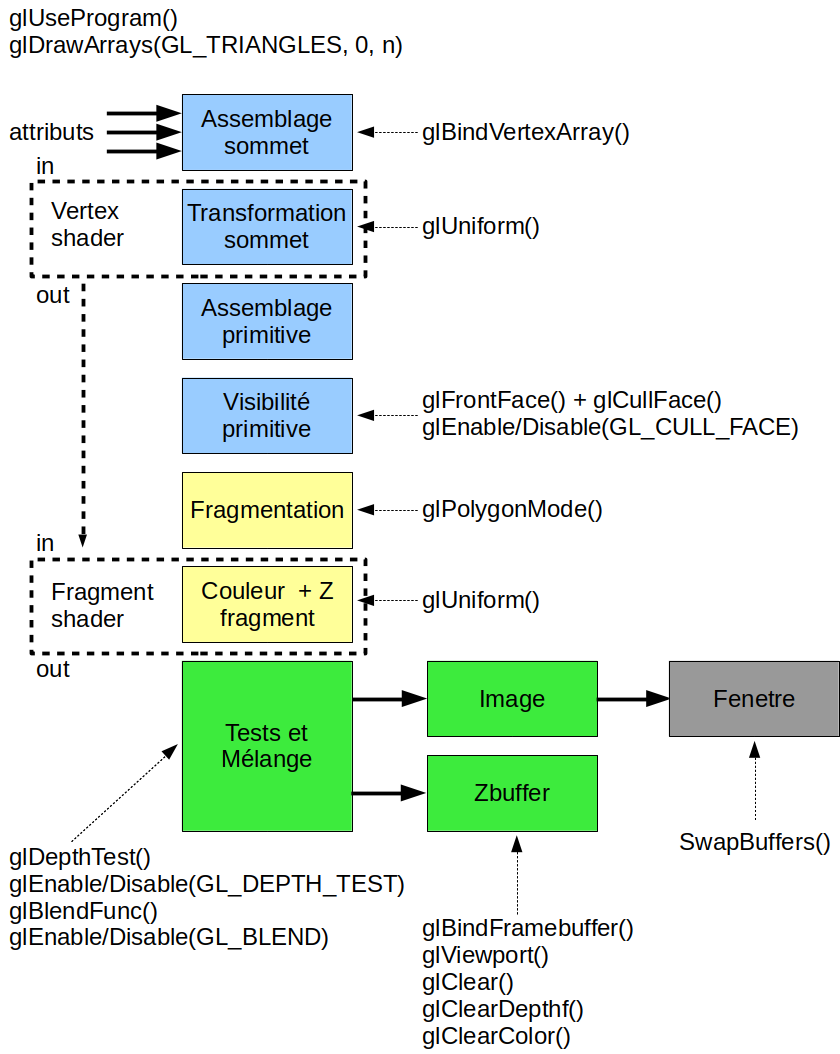
pour dessiner un triangle (ou plusieurs), il faut donc paramétrer le pipeline, en utilisant les fonctions de l'api openGL, pour obtenir le résultat voulu... cf afficher plusieurs triangles, modifier les paramètres uniform d'un shader program et écrire les 2 shaders... cf shaders et GLSL N'oubliez pas que tout ça est juste une manière très maladroite d'exécuter des shaders sur le gpu / processeurs de la carte graphique : glDraw(GL_TRIANGLES, n) peut vraiment se comprendre comme :

suite de la lecture :

Generated on Fri Dec 1 2023 13:25:53 for gKit2 light by doxygen 1.9.1