shader et brdf

Tous les modèles de matières s'utilisent de la même manière. Ils permettent de connaitre la lumière réfléchie vers une direction, l'observateur, par exemple :

\[L_r(p, \vec{o})= f_r(\vec{l}, \vec{o}) \cdot L_i(p, \vec{l}) \cos \theta_l \]

La lumière \( L_i(p, \vec{l}) \) arrive sur le point p depuis la direction \(\vec{l}\) et le modèle de matière, la brdf \(f_r(\vec{l}, \vec{o})\) indique quelle quantité \(L_r(p, \vec{o})\) est réfléchie par p dans la direction \(\vec{o}\).

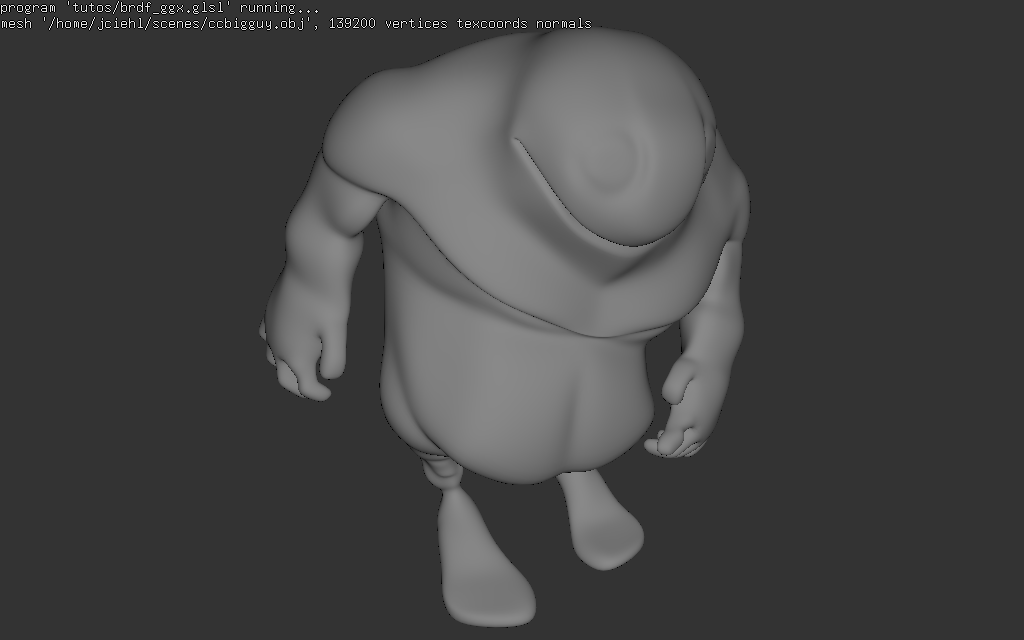
premier shader : matière diffuse, modèle de Lambert

\[ f_r(\vec{o}, \vec{l})= \frac{k}{\pi}\]

remarque : pourquoi le \( \frac{1}{\pi} \) ? les modèles de matières doivent vérifier quelques propriétés. Les détails sont dans la partie modèles réalistes.

donc oui, ce "modèle" de réflexion est une constante k comprise entre 0 et 1 qui représente à quel point la matière réfléchit la lumière incidente. Et comme il est indépendant de la direction d'observation, la même quantité de lumière est réfléchie dans toutes les directions.

comment on fait ?

on doit calculer :

\[L_r(p, \vec{o})= \frac{k}{\pi} \cdot L_i(p, \vec{l}) \cos \theta_l \]

il suffit de calculer \( \cos \theta_l \), le cosinus de l'angle entre la normale en p et la direction vers la lumière, et de se rappeler que les calculs sur les points et les vecteurs doivent se faire avec des coordonnées dans le même repère.

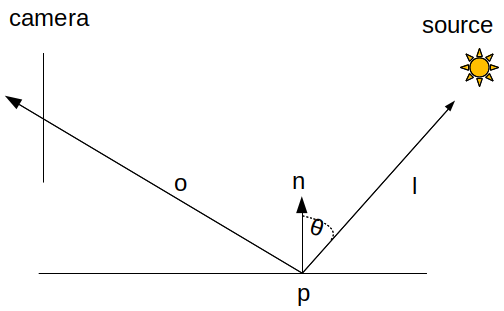
en résumé, il faut connaitre, dans le même repère :

• p, la position du point éclairé,
• \( \vec{n} \), la normale de la surface au point p,
• \( \vec{o} \), la direction du point p vers l'observateur, la camera,
• \( \vec{l} \), la direction du point p vers la source de lumière,
• k, la constante de modèle de réflexion.

premier constat, les normales et les positions doivent faire partie de la description des sommets de l'objet. elles sont donc accessibles par le vertex shader, mais pas directement par le fragment shader.

la position de la camera, la position de la source de lumière, son emission et la constante k, seront des uniforms du fragment shader.

comment obtenir p et n dans le fragment shader ?

il suffit de se rappeler que les sorties du vertex shader sont interpolées avant d'être accessibles par le fragment shader. l'interpolation des positions des sommets du triangle calcule, pour chaque pixel, la position dans l'espace du point du triangle se projettant sur le centre du pixel. pour les normales, il ne faut pas oublier que l'interpolation change la longueur des vecteurs. le vertex shader déclare 2 sorties, des varyings : out vec3 p; out vec3 n; il ne reste plus qu'à calculer leurs coordonnées dans un repère commun...

quel repère pour les calculs ? n'importe quel repère avant la projection : repère objet, scène ou camera. la projection ne préserve par les angles, et comme on doit en calculer plusieurs, autant choisir un repère dans lequel c'est simple à faire.

remarque : repassez dans introduction api 3d, openGL et pipeline graphique ou le cm d'intro openGL, si nécessaire.

les exemples suivants font les calculs dans le repère du monde, mais ce n'est peut être pas le plus efficace. pourquoi ?

on suppose que l'on connait la position de la source et la position de la camera dans le repère du monde, donc pas de transformation. pour les sommets et les normales, par contre, on connait leur coordonnées dans le repère de l'objet, il faut donc les transformer, en utilisant la matrice model.

#version 330
 
// vertex shader
in vec3 position;               // attribut, repere local de l'objet
in vec3 normal;                 // attribut, repere local de l'objet
 
uniform mat4 mvpMatrix;         // transformation du repere local de l'objet vers le repere projectif
uniform mat4 modelMatrix;       // transformation du repere local de l'objet vers le repere du monde / de la scene
 
out vec3 p;                     // varying, sortie : position dans le repere du monde 
out vec3 n;                     // varying, sortie : normale dans le repere du monde
 
void main( )
{
    // resultat obligatoire du vertex shader, position dans le repere projectif
    gl_Position= mvpMatrix * vec4(position, 1);
    
    // calcule la position et la normale du sommet dans le repere du monde, et le transmet au fragment shader,
    // necessaire pour calculer la lumiere reflechie
    p= vec3(modelMatrix * vec4(position, 1));
    n= vec3(modelMatrix * vec4(normal, 0));
    
    /* remarque : on peut decomposer toutes les etapes 
        vec4 p4= modelMatrix * vec4(position, 1);
        vec4 n4= modelMatrix * vec4(normal, 0);
        p= p4.xyz / p4.w;
        n= n4.xyz;
        
        mais, comme il n'y a de projection dans la transformation utilisee, p4.w == 1 
        et comme normal est une direction n4.w == 0...
     */
    
    /* remarque : il pas necessaire d'utiliser la matrice homogene 4x4 pour transformer un vecteur. on peut aussi ecrire :
        n= mat3(modelMatrix) * normal;
        
        directement en utilisant que la partie 3x3 de la matrice
     */
}

il ne reste plus qu'à écrire le fragment shader qui doit calculer les directions \( \vec{o} \) et \( \vec{l} \) et \( \cos \theta_l \) :

#version 330
 
// fragment shader
in vec3 p;                      // varying, entree : position dans le repere du monde, cf vertex shader
in vec3 n;                      // varying, entree : normale dans le repere du monde, cf vertex shader
 
uniform vec3 camera;            // uniform : position de la camera dans le repere du monde, affecte par l'application
uniform vec3 source;            // uniform : position de la source de lumiere dans le repere du monde, affecte par l'application
uniform vec3 emission;          // uniform : emission de la source de lumiere (couleur rgb), affecte par l'application
uniform float k;                // uniform : parametre de la brdf, affecte par l'application
 
const float PI= 3.14159265359;      
 
out vec4 fragment_color;        // sortie du fragment shader, couleur du fragment / pixel
void main( )
{
    // directions 
    vec3 o= normalize(camera - p);
    vec3 l= normalize(source - p);
    vec3 nn= normalize(n);
    
    // cos
    float cos_theta= dot(nn, l);
    
    // brdf
    float fr= k / PI;
    vec3 color= fr * emission * cos_theta;
    
    fragment_color= vec4(color, 1);
}

une relation utile : \( \cos \angle(\vec{u}, \vec{v})= \frac{\vec{u} \cdot \vec{v}}{||\vec{u}|| \cdot ||\vec{v}||} \), ce qui s'écrit directement : float cos_theta= dot(normalize(u), normalize(v));

autre remarque : les normales devraient être transformées par une matrice différente de celles des sommets. dans les cas simples, lorsqu'il n'y a pas d'étirement ou de changement d'échelle dans la transformation des sommets, les normales subissent la même transformation. sinon Transform::normal() renvoie la transformation à utiliser sur les normales.

ce shader suppose que le flux émis par la source arrive intégralement en p, ce qui est faux, il manque un terme \( 1 / ||\vec{l}||^2 \) et un cosinus si la source n'est pas un point. cf le cours simulation et integration numérique.

vous pouvez tester avec shader_kit, cf prototyper un shader program :
bin/shader_kit tutos/brdf_lambert.glsl data/bigguy.obj

premier reflets : modèle de Blinn - Phong

La démarche est identique, on doit calculer :

\[L_r(p, \vec{o})= \frac{\alpha+8}{8\pi} \cos^\alpha \theta_h \cdot L_i(p, \vec{l}) \cos \theta_l \]

il faut connaitre, dans le même repère :

• p, la position du point éclairé,
• \( \vec{n} \), la normale de la surface au point p,
• \( \vec{o} \), la direction du point p vers l'observateur, la camera,
• \( \vec{l} \), la direction du point p vers la source de lumière,
• \( \vec{h} \), la direction bisectrice de \( \vec{o} \) et \( \vec{l} \),
• \( \alpha \), le paramètre de concentration du reflet, dit l'exposant...

le fragment shader doit calculer les directions \( \vec{o} \), \( \vec{l} \), et \( \vec{h} \), puis \( \cos \theta_l \) et \( \cos \theta_h \) :

// parametres
uniform float alpha;
 
    // directions
    vec3 o= normalize(camera - p);
    vec3 l= normalize(source - p);
    vec3 h= normalize(o + l);
    vec3 nn= normalize(n);
    
    // cos
    float cos_theta= max(0, dot(nn, l));
    float cos_theta_h= dot(nn, h);
    
    // brdf
    float fr= (alpha+8) / (8*PI) * pow(cos_theta_h, alpha);
    vec3 color= emission * fr * cos_theta;    

reflets réalistes : modèle à microfacettes

Un modèle à microfacettes se présente classiquement sous cette forme :

\[ f_r(\vec{o}, \vec{l})= \frac{F(\vec{o}, \vec{h}) \, D(\vec{h}) \, G_2(\vec{o}, \vec{l}, \vec{h}) }{4 |\vec{n} \cdot \vec{o}| |\vec{n} \cdot \vec{l}|} \]

Le terme \( F \), le coefficient de Fresnel, représente le reflet crée par une facette, \( D \) correspond au nombre de facettes orientées dans la direction \( \vec{h} \) et qui créent l'intensité du reflet (plus il y a de micro-facettes orientées dans la bonne direction, plus le reflet est intense). Le reste, \( G_2 \) et le cosinus \( |\vec{n} \cdot \vec{o}| \) permettent de normaliser \( D \) pour garantir la conservation d'énergie.

\[ D( \vec{h} ) = \frac{\chi^+(\vec{h} \cdot \vec{n})}{\pi \alpha^2 \cos^4 \theta_m \left( 1 + \frac{\tan^2 \theta_h}{\alpha^2} \right)^2 }, \textrm{ cf Heitz 2014, eq 71}\\ \]

\begin{eqnarray*} G_2( \vec{o}, \vec{l}, \vec{h} ) & = & \frac{\chi^+(\vec{o} \cdot \vec{h}) \chi^+(\vec{l} \cdot \vec{h})} {1 + \Lambda(\vec{o}) + \Lambda(\vec{l})}, \textrm{ cf Heitz 2014, eq 99}\\ \textrm{ avec}& : &\\ \Lambda(\vec{\omega}) & = & - \frac{1}{2} + \frac{1}{2} \sqrt{1 + \alpha^2 \tan^2 \theta}, \textrm{ cf Heitz 2014, eq 72}\\ \textrm{ et}& : &\\ \chi^+(x) & = & 0 \textrm{ si } x < 0\\ & = & 1 \textrm{ sinon } \end{eqnarray*}

Bon, ca fait pas mal de termes à évaluer, première étape, lesquels peut-on calculer facilement ?

rappel : on sait calculer facilement \( cos \angle(\vec{u}, \vec{v}) \) :

• \( \sin^2 \theta + \cos^2 \theta = 1 \textrm{ donc } \sin^2 \theta = 1 - \cos^2 \theta \textrm{ et } \sin \theta = \sqrt{1 - \cos^2 \theta} \)
• \( \tan^2 \theta = \frac{\sin^2 \theta}{\cos^2 \theta} \textrm{ donc } \tan^2 \theta = \frac{1 - \cos^2 \theta}{\cos^2 \theta} \textrm{ ou } \tan^2 \theta = \frac{1}{\cos^2 \theta} -1\)

après quelques manipulations on arrive à :

\[ D( \vec{h} ) = \chi^+(\vec{h} \cdot \vec{n}) \frac{\alpha^2}{\pi \left( 1 + \cos^2 \theta_h (\alpha^2 -1) \right)^2} = \chi^+(\vec{h} \cdot \vec{n}) \frac{1}{\pi} \left( \frac{\alpha}{1 + \cos^2 \theta_h (\alpha^2 -1)} \right)^2 \]

ensuite on peut re-écrire \( \Lambda(\vec{\omega}) = - \frac{1}{2} + \frac{1}{2} \sqrt{1 + \alpha^2 \tan^2 \theta_\omega} = - \frac{1}{2} + \frac{1}{2} \sqrt{1 + \alpha^2 \left( \frac{1}{\cos^2\theta_\omega} -1 \right)} \) et :

\[ G_2( \vec{o}, \vec{l}, \vec{h} ) = \chi^+(\vec{o} \cdot \vec{h}) \chi^+(\vec{l} \cdot \vec{h}) \frac{2}{\sqrt{1 + \alpha^2 \tan^2 \theta_o} + \sqrt{1 + \alpha^2 \tan^2 \theta_l}} \]

La démarche est toujours la même, on doit calculer :

\[L_r(p, \vec{o})= \frac{F(\vec{o}, \vec{h}) \, G_2(\vec{o}, \vec{l}, \vec{h}) \, D(\vec{h})}{4 |\vec{n} \cdot \vec{o}| |\vec{n} \cdot \vec{l}|} \cdot L_i(p, \vec{l}) \cos \theta_l \]

Les paramètres du modèle sont la rugosité \( \alpha \) ainsi que l'indice de réfraction \( \eta \), ou \( F_0 \) (on peut calculer l'un en fonction de l'autre), il ne reste plus qu'à évaluer les termes :

// parametres
uniform vec3 F0;
uniform float alpha;
 
    // directions
    vec3 o= normalize(camera - p);
    vec3 l= normalize(source - p);
    vec3 h= normalize(o + l);
    
    // cos
    vec3 nn= normalize(n);
    float cos_theta= max(0, dot(nn, l));
    float cos_theta_h= max(0, dot(nn, h));
    float cos_theta_o= max(0, dot(nn, o));
    
    // meme hemisphere
    vec3 color= vec3(0);
    if(cos_theta > 0 && cos_theta_h > 0 && cos_theta_o > 0)
    {
        // D
        float D= alpha / (1 + cos_theta_h*cos_theta_h * (alpha*alpha -1));
        D= D*D / PI;
        
        // G2
        float tan2_theta_o= 1 / (cos_theta_o*cos_theta_o) - 1;
        float lambda_o= 1 + alpha*alpha * tan2_theta_o;
        float tan2_theta= 1 / (cos_theta*cos_theta) - 1;
        float lambda= 1 + alpha*alpha * tan2_theta;
        float G2= 2 / (sqrt(lambda_o) + sqrt(lambda));
        
        // F
        float F= F0 + (1 - F0) * pow(1 - dot(o, h), 5);
        
        // brdf
        float fr= (F * D * G2) / (4 * cos_theta_o * cos_theta);
        color= emission * fr * cos_theta;
    }

exemples

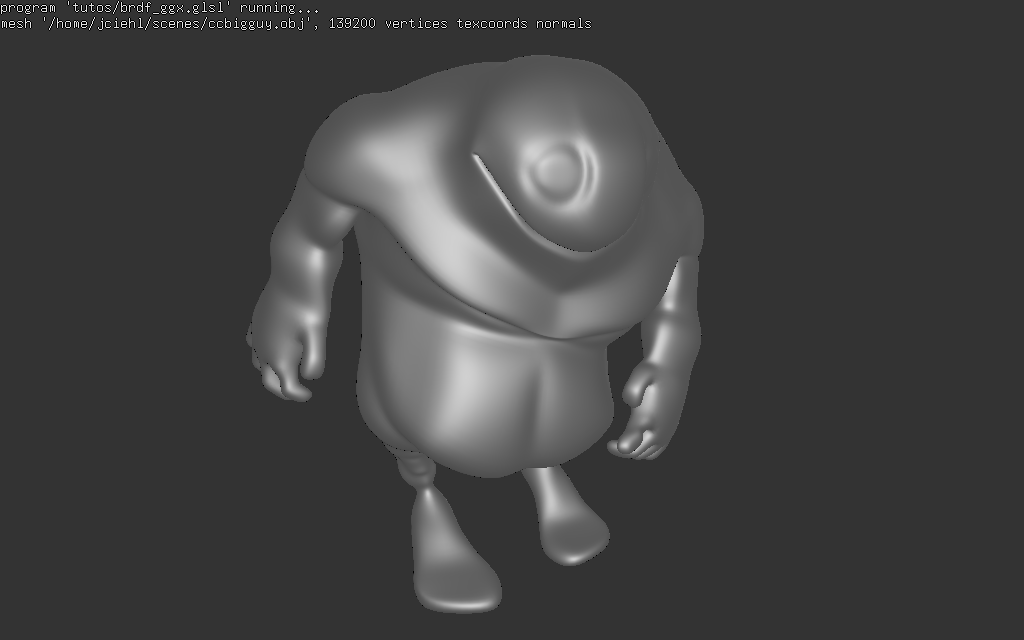quelques exemples de reflets pour Blinn - Phong et ce modèle à microfacettes :