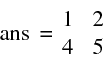1.3 Notations matricielles de Matlab

Une chose importante à comprendre est que tous les objets sous Matlab sont des matrices, et que Matlab les traite efficacement si on utilise les notations matricielles:

• un scalaire est une matrice de dimension (1,1),
• un vecteur ligne de n composantes est une matrice de dimension (1,n),
• un vecteur colonne de m composantes est une matrice de dimension (m,1).

Attention Matlab fait la distinction entre un vecteur ligne et un vecteur colonne !

Pour définir une matrice, on utilise les symboles pour délimiter le début et la fin des éléments, l'espace (ou la virgule ) pour séparer les valeurs sur une ligne et le symbole pour délimiter les lignes. Ainsi l'instruction

>> A = [ 1 2 3; 4 5 6]

A = $\begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6\end{array}$

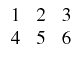
définit une matrice A de dimension 2*3.

>>B= [1 2 3]

B= $\begin{array}{ccc} 1 & 2 & 3\end{array}$

définit un vecteur ligne de dimension 1*3.

>>C=[1;2]

C= $\begin{array}{c} 1\\ 2\end{array}$

définit un vecteur colonne de dimension 2*1. On peut vérifier ces définitions avec la fonction whos , qui liste les variables définies par l'utilisateur avec leurs tailles respectives.

>>whos

Name    Size       Bytes Class

A       2x3    48 double array

B      1x3   24 double array

C      2x1   16 double array

Grand total is 11 elements using 88 bytes

Pour calculer la transposée d'un vecteur ou d'une matrice, on utilise le symbole apostrophe

>>C'

$$\mbox{ans\, =}1\,2$$

Pour sélectionner une partie d'un vecteur ou d'une matrice, on utilise la notation d'intervalle . On peut ne pas spécifier l'indice $i$ de début (la valeur par défaut est alors 1) ou l'indice $j$ de fin (la valeur par défaut est la dimension du tableau).

>>A(:,1:2)

$$\mbox{ans\, =}\begin{array}{cc} 1 & 2\\ 4 & 5\end{array}$$