suivant: 1.5 Fonctions mathématiques monter: 1. Introduction à Matlab précédent: 1.3 Notations matricielles de Table des matières
Les opérateurs arithmétiques s'appliquent aux scalaires, aux vecteurs et aux matrices. Il faut juste vérifier que les opérandes soient compatibles.
L' opérateur d'addition est noté ![]() et celui de la soustraction
et celui de la soustraction
![]() .
.
Pour la multiplication, on distingue la multiplication matricielle,
le produit scalaire et le produit tensoriel notés tous ![]() ,
et la multiplication terme à terme notée
,
et la multiplication terme à terme notée ![]() .
.
>> A*B' multiplication matricielle
(2x3) x (3,1)=>(2,1)
![]()
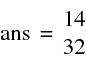
>> B*B' produit scalaire (1,3)x(3,1)=>(1,1)
![]()
>> A1=C*C' produit tensoriel
(2,1)x(1,2)=>(2,2) ![]()
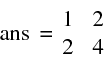
Donc le produit ![]() n'est possible que si A a un nombre
de colonnes égale au nombre de lignes de B. Le résultat est
une matrice dont le nombre de lignes est égale à celui de A
et le nombre de colonnes à celui de B. Si cela n'est pas
le cas, on obtiens une erreur:
n'est possible que si A a un nombre
de colonnes égale au nombre de lignes de B. Le résultat est
une matrice dont le nombre de lignes est égale à celui de A
et le nombre de colonnes à celui de B. Si cela n'est pas
le cas, on obtiens une erreur:
>> B*B
??? Error using ==> *
Inner matrix dimensions must agree.
La multiplication terme à terme correspond à la multiplication des coefficients, et se fait avec des opérandes de même dimension.
>> B.*B
De la même façon, l'opérateur d'élévation à une puissance peut s'écrire
de 2 façons
![]() ou
ou
![]() :
:
>>A1^2 correspond à A1*A1
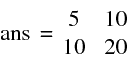
>>A1.^2 correspond à l'élévation au carré des coefficients de A1
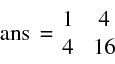
Pour la division, on distingue la division matricielle à droite ![]() ,
i.e. la multiplication par l'inverse de l'opérande droit, et la division
matricielle à gauche
,
i.e. la multiplication par l'inverse de l'opérande droit, et la division
matricielle à gauche
![]() , i.e. la multiplication
par l'inverse de l'opérande gauche:
, i.e. la multiplication
par l'inverse de l'opérande gauche:
>>A=[2 -1; -1 2];B=[0;3];
>>X=A\B; résolution
de ![]() , i.e.
, i.e. ![]()
>>Y=B/A; résolution de ![]() ,
i.e.
,
i.e. ![]()
Les opérateurs de division terme à terme sont notés ![]() et
et
![]()