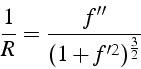suivant: 3.3 Fonctions Maple monter: 3. Courbes dans le précédent: 3.1 Courbe Table des matières
Trajectoire=courbe paramétrée par le temps ![]()
Soit ![]() un point de la trajectoire :
un point de la trajectoire :
Tangente à la trajectoire
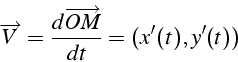
Accélération
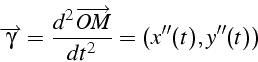
![]() abscisse curviligne,
abscisse curviligne,
![]()
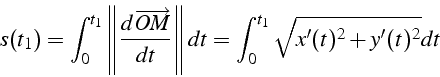
distance parcourue pendant ![]()
En un point ![]() de la trajectoire, c'est le repère
de la trajectoire, c'est le repère
![]() orthonormée directe où
orthonormée directe où
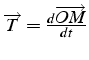 est le vecteur unitaire tangent (i.e. //
est le vecteur unitaire tangent (i.e. //![]() à la vitesse):
à la vitesse):
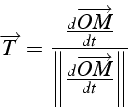
![]() le vecteur est orthogonal directe t.q
le vecteur est orthogonal directe t.q
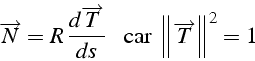
![]() est le rayon de courbure de la trajectoire en
est le rayon de courbure de la trajectoire en ![]() (la courbure
(la courbure
![]() )
)
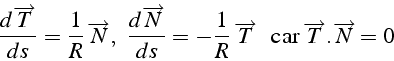
![\includegraphics[width=0.6\paperwidth]{CHAP2/frenet}](img123.png)
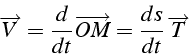
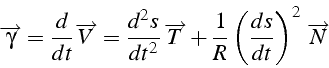
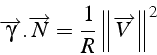
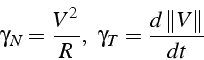
![\includegraphics[width=0.6\paperwidth]{CHAP2/accel}](img128.png)
Dans le cas d'une courbe plane ![]() , le repére de Frenet s'écrit:
, le repére de Frenet s'écrit:
![\begin{displaymath}
\overrightarrow{T}=\left[\begin{array}{cc}
\frac{1}{\sqrt{(1...
...sqrt{(1+f'^{2})}} & \frac{1}{\sqrt{1+f'^{2}}}\end{array}\right]\end{displaymath}](img129.png)
et la courbure s'écrit en fonction de ![]()