suivant: 7.3 Paramètres du calcul monter: 7. Refroidissement d'un micro-processeur précédent: 7.1 Problème Table des matières
On a donc à résoudre dans chaque domaine l'équation de la chaleur 2D instationnaire:
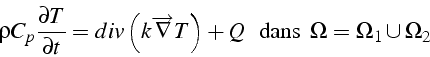
avec des valeurs de ![]() ,
, ![]() et
et ![]() différentes dans chacun
des domaines. Le terme source
différentes dans chacun
des domaines. Le terme source ![]() vaut:
vaut:
dans ![]() et
et ![]() dans
dans ![]() . On note
. On note ![]() la
longueur du radiateur et
la
longueur du radiateur et ![]() sa hauteur.
sa hauteur.
La condition initiale correspond à un composant hors tension, et donc une température égale à la température extérieure:
Les conditions aux limites sont les suivantes:
A l'état stationnaire, on a
qui intégré sur ![]() donne, compte tenu des conditions aux limites:
donne, compte tenu des conditions aux limites:
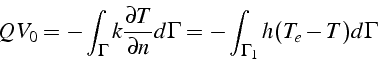
On a noté ![]() le volume (par unité de longueur en z) du domaine
le volume (par unité de longueur en z) du domaine
![]() . En notant
. En notant ![]() la surface (par unité de longueur
en z) de la frontière
la surface (par unité de longueur
en z) de la frontière ![]() où l'on a un échange de chaleur
par convection, la température moyenne
où l'on a un échange de chaleur
par convection, la température moyenne ![]() du radiateur à l'état
stationnaire vérifie:
du radiateur à l'état
stationnaire vérifie:
Soit avec les données du problème ![]() ,
, ![]() ,
,
![]()
De la même façon, en intégrant l'équation d'équilibre en temps et
en espace entre l'instant initial ![]() et l'instant ou l'on atteint
l'état stationnaire
et l'instant ou l'on atteint
l'état stationnaire ![]() :
:
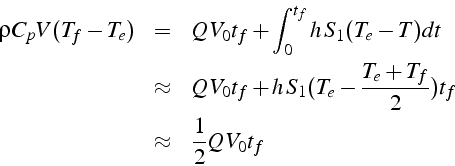
ce qui fournit une estimation du temps ![]() pour atteindre l'état
stationnaire (on note
pour atteindre l'état
stationnaire (on note ![]() le volume du radiateur):
le volume du radiateur):
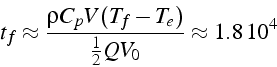
On choisit donc un temps d'intégration des équations de ![]() (
(![]() ).
).