suivant: 4.2 Première approche avec monter: 4. Méthode des éléments précédent: 4. Méthode des éléments Table des matières
On considère l'écoulement d'un fluide incompressible (air à des faibles
vitesses d'écoulement), de masse volumique ![]() constante, autour
d'un obstacle cylindrique de rayon R et d'axe Oz.
constante, autour
d'un obstacle cylindrique de rayon R et d'axe Oz.
L'écoulement est à deux dimensions (vitesses parallèles au plan xOy
et indépendantes de z) et stationnaire. Un point M du plan xOy est
repéré par ses coordonnées polaires ![]() . L'obstacle, dans
son voisinage, déforme les lignes de courant ; loin de l'obstacle,
le fluide est animé d'une vitesse uniforme
. L'obstacle, dans
son voisinage, déforme les lignes de courant ; loin de l'obstacle,
le fluide est animé d'une vitesse uniforme ![]() suivant Ox.
suivant Ox.
![\includegraphics[width=0.6\textwidth]{CHAP1/cylind}](img113.png)
L'écoulement est supposé irrotationnel, et le fluide est supposé parfait (viscosité nulle).
Dans ce cas l'écoulement est un écoulement potentiel, c.a.d que la
vitesse découle d'un champ potentiel ![]() :
:
![\begin{displaymath}
\overrightarrow{U}=\overrightarrow{grad} \Phi=\left[\begin{...
...partial x}\\
\frac{\partial\Phi}{\partial y}\end{array}\right]\end{displaymath}](img115.png)
qui vérifie une équation de Laplace:
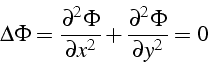
Les conditions aux limites sont telles que loin de l'obstacle la vitesse
est égale à ![]() , et que le fluide glisse sur l'obstacle, c.a.d.
que la vitesse normale est nulle
, et que le fluide glisse sur l'obstacle, c.a.d.
que la vitesse normale est nulle
![]() .
La solution analytique de ce problème peut être calculée avec la théorie
des fonctions conformes:
.
La solution analytique de ce problème peut être calculée avec la théorie
des fonctions conformes:
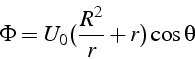
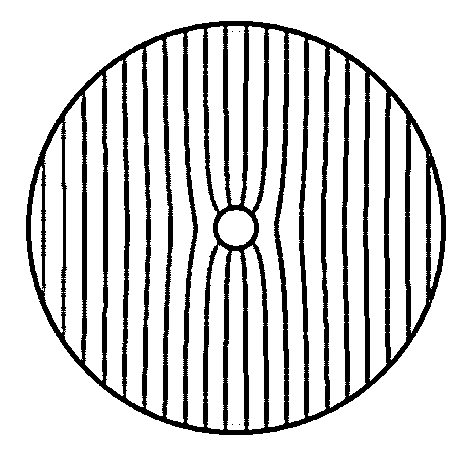
Cette solution est tracée sur la figure ci-dessous. Le champ de vitesse
est perpendiculaire aux lignes de potentiel (
![]() est parallèle à
est parallèle à
![]() ).
).
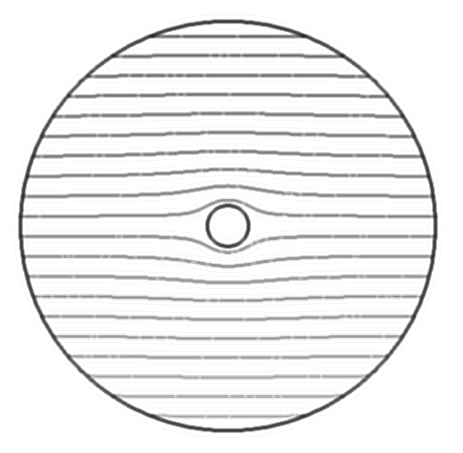
Cette fonction potentielle ![]() est associée à une fonction orthogonale
est associée à une fonction orthogonale
![]() (tracée ci-dessus), telle que
(tracée ci-dessus), telle que
![\begin{displaymath}
\overrightarrow{U}=\left[\begin{array}{c}
\frac{\partial\P...
...artial y}\\
-\frac{\partial\Psi}{\partial x}\end{array}\right]\end{displaymath}](img123.png)
Cette fonction ![]() est la fonction de courant de l'écoulement,
i.e. les lignes
est la fonction de courant de l'écoulement,
i.e. les lignes ![]() sont des lignes tangentes au vecteur
vitesse (
sont des lignes tangentes au vecteur
vitesse (
![]() ). L'écoulement
étant stationnaire, ces lignes correspondent aux trajectoires des
particules fluides. On montre facilement que
). L'écoulement
étant stationnaire, ces lignes correspondent aux trajectoires des
particules fluides. On montre facilement que ![]() vérifie aussi
une équation de Laplace:
vérifie aussi
une équation de Laplace:
Les conditions aux limites associées sont:
Pour résoudre ce problème par élément finis, on choisit un domaine
de calcul ![]() fini: i.e. la frontière
fini: i.e. la frontière ![]() est ramenée
à une distance finie
est ramenée
à une distance finie ![]() du cylindre (à cette distance la perturbation
due au cylindre est négligeable):
du cylindre (à cette distance la perturbation
due au cylindre est négligeable):
![]() . On note
. On note
![]() la frontière extérieure et
la frontière extérieure et
![]() la frontière du cylindre.
la frontière du cylindre.
On découpe le domaine ![]() en
en ![]() éléments triangulaires
(triangulation):
éléments triangulaires
(triangulation):
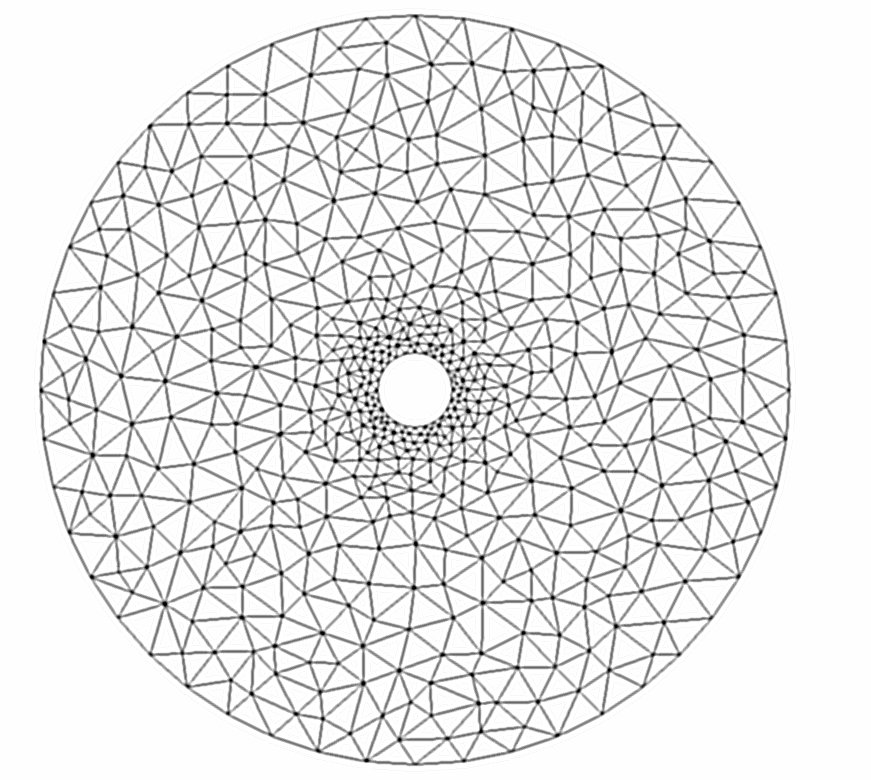
A partir de ce maillage, on construit ensuite une solution approchée
![]() comme une approximation polynomiale par morceaux.
Ainsi avec une approximation quadratique (élément finis
comme une approximation polynomiale par morceaux.
Ainsi avec une approximation quadratique (élément finis ![]() ),
sur chaque élément
),
sur chaque élément ![]() , la solution est un polynôme de degré
2 en x et y:
, la solution est un polynôme de degré
2 en x et y:
et possède donc 6 degrés de liberté, qui sont les 3 valeurs aux sommets de l'élément et les 3 valeurs sur les milieux de cotés
![\includegraphics[width=0.4\textwidth]{CHAP1/elt2d}](img137.png)
Compte tenu des conditions aux limites et de la continuité inter-éléments,
la solution ![]() possède
possède ![]() degrés de liberté (ce nombre
dépend du nombre d'éléments et du nombre de noeuds sur les frontières)
et s'écrit:
degrés de liberté (ce nombre
dépend du nombre d'éléments et du nombre de noeuds sur les frontières)
et s'écrit:
Le terme en ![]() permet de vérifier les conditions aux limites
5.2:
permet de vérifier les conditions aux limites
5.2:
Pour déterminer les valeurs inconnues ![]() , on écrit la formulation
faible de la méthode des résidues pondérés, en multipliant l'équation
5.1 par une fonction test
, on écrit la formulation
faible de la méthode des résidues pondérés, en multipliant l'équation
5.1 par une fonction test ![]() , puis en intégrant
sur le domaine
, puis en intégrant
sur le domaine ![]() :
:
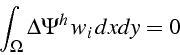
On intègre par partie, en utilisant la formule de Green, pour obtenir la relation suivante:
En utilisant la méthode de Galerkin, les fonctions tests ![]() sont les fonctions de base
sont les fonctions de base ![]() associées au degré de liberté
de
associées au degré de liberté
de ![]() :
:
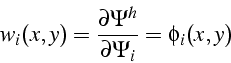
Ces fonctions tests s'annulent sur la frontière ![]() de
de ![]() ,
et donc l'intégrale de bord dans 5.4 est nulle. En remplaçant
,
et donc l'intégrale de bord dans 5.4 est nulle. En remplaçant
![]() par son expression 5.3 , cette équation 5.4
s'écrit:
par son expression 5.3 , cette équation 5.4
s'écrit:
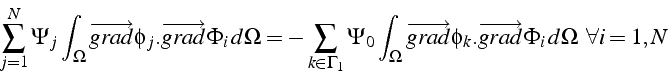
qui est un système linéaire de ![]() équations pour
équations pour ![]() inconnues
inconnues
![]() qu'il suffit de résoudre pour obtenir la solution
approchée
qu'il suffit de résoudre pour obtenir la solution
approchée ![]() .
.