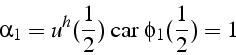suivant: 3.3 Méthode des éléments monter: 3. Introduction aux éléments précédent: 3.1 Introduction Table des matières
La méthode des résidus pondérés est une méthode générale de recherche de solutions approchées d'équations différentielles ou aux dérivées partielles
Considérons par exemple, le problème
![]() suivant:
suivant:
trouvez la solution ![]() de l'équation
de l'équation
associée aux conditions aux limites:
Le problème
![]() n'admet pas forcément une solution
analytique explicite3.1 pour toutes les fonctions
n'admet pas forcément une solution
analytique explicite3.1 pour toutes les fonctions ![]() . On va donc chercher une approximation
. On va donc chercher une approximation
![]() de la solution exacte
de la solution exacte ![]() de
de
![]() .
.
De façon générale, on va chercher cette approximation ![]() comme une combinaison linéaire
comme une combinaison linéaire ![]() de fonctions de base
de fonctions de base ![]() :
:
Les fonctions de base ![]() étant connues, il faut donc déterminer
les coefficients
étant connues, il faut donc déterminer
les coefficients ![]() pour déterminer la solution approchée
pour déterminer la solution approchée
![]() .
.
Pour que la solution ![]() vérifie les conditions aux limites
3.2, on impose dans ce cas aux fonctions de base de vérifier
ces conditions aux limites.
vérifie les conditions aux limites
3.2, on impose dans ce cas aux fonctions de base de vérifier
ces conditions aux limites.
Par contre, on ne peut en général pas trouver les coefficients ![]() telle que la solution approchée 3.3 vérifie l'équation 3.1
. En effet si
telle que la solution approchée 3.3 vérifie l'équation 3.1
. En effet si ![]() vérifie l'équation 3.1, alors
vérifie l'équation 3.1, alors ![]() est la solution exacte
est la solution exacte ![]() !
!
L'équation 3.1 n'étant pas vérifiée exactement pas les solutions
3.3, on va essayer de déterminer la meilleur approximation
![]() , i.e. celle correspondant à une erreur la plus petite
dans l'équation. Pour cela on définit le résidu
, i.e. celle correspondant à une erreur la plus petite
dans l'équation. Pour cela on définit le résidu ![]() de l'équation
3.1 :
de l'équation
3.1 :
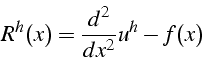
et on impose que ce résidu soit nul dans un certain espace ![]() (de dimension
(de dimension ![]() ). Soit
). Soit
![]() une base de fonctions
de
une base de fonctions
de ![]() , cette condition est la condition d'orthogonalité de
, cette condition est la condition d'orthogonalité de ![]() par rapport à
par rapport à ![]() :
:
en notant ![]() le produit scalaire de 2 fonctions
le produit scalaire de 2 fonctions ![]() et
et ![]() .
.
En remplaçant ![]() en fonction de
en fonction de ![]() donné par 3.3,
il vient:
donné par 3.3,
il vient:
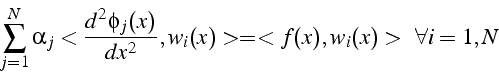
C'est un système linéaire de ![]() équations à
équations à ![]() inconnues
inconnues
![]() :
:
qu'il suffit de résoudre pour obtenir la solution approchée de 3.1.
On remarque aussi que le nombre de fonctions tests ![]() doit bien
être égale au nombre de degré de liberté
doit bien
être égale au nombre de degré de liberté ![]() de la solution
approchée, pour que le problème approchée admette une solution unique.
de la solution
approchée, pour que le problème approchée admette une solution unique.
Cette approche très générale de résolution d'une équation différentielle
consiste donc à remplacer la recherche d'une solution analytique de
3.1 par un problème discret 3.4 plus simple de dimension
![]() , qui dans le cas étudié est le système linéaire 3.5.
, qui dans le cas étudié est le système linéaire 3.5.
Dans la pratique, il reste cependant à déterminer les fonctions de
base ![]() , les fonctions tests
, les fonctions tests ![]() et le produit
scalaire
et le produit
scalaire ![]() .
.
Pour le produit scalaire ![]() de 2 fonctions, on choisit l'intégrale
sur le domaine du produit des 2 fonctions définie par:
de 2 fonctions, on choisit l'intégrale
sur le domaine du produit des 2 fonctions définie par:
On vérifie que c'est un produit scalaire (c'est la généralisation
du produit scalaire euclidien dans
![]() ), qui définie
une norme (équivalente à la norme euclidienne dans
), qui définie
une norme (équivalente à la norme euclidienne dans
![]() ):
):
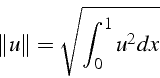
La méthode des résidus pondérés s'écrit alors:
Dans la méthode de Galerkin, on choisit comme fonctions tests ![]() les fonctions de base
les fonctions de base ![]() de l'approximation.
de l'approximation.
Comme base de fonctions ![]() , on choisit une famille de
fonctions trigonométriques vérifiant les conditions aux limites 3.1,
i.e.:
, on choisit une famille de
fonctions trigonométriques vérifiant les conditions aux limites 3.1,
i.e.:
Ainsi, pour ![]() , la solution approchée s'écrit:
, la solution approchée s'écrit:
où ![]() est solution de l'équation scalaire
est solution de l'équation scalaire
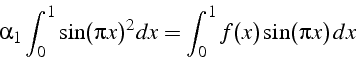
qui s'écrit en remplaçant ![]() par son expression et en calculant
les intégrales:
par son expression et en calculant
les intégrales:
La solution obtenue est comparée à la solution exacte sur la figure ci dessous.
![\includegraphics[width=0.5\textwidth]{CHAP1/uh}](img70.png)
Pour montrer que la solution obtenue est la meilleure approximation
![]() de la forme 3.8, on a tracé l'erreur entre la solution
exacte et des solutions
de la forme 3.8, on a tracé l'erreur entre la solution
exacte et des solutions ![]() (3.8) pour plusieurs valeurs
de
(3.8) pour plusieurs valeurs
de ![]() proche de la valeur optimale 3.9.
proche de la valeur optimale 3.9.
![\includegraphics[width=0.5\textwidth]{CHAP1/errh}](img71.png)
On peut augmenter la précision de l'approximation en augmentant le
nombre ![]() de fonctions de base. Par exemple pour
de fonctions de base. Par exemple pour ![]() on obtiens
une solution plus précise comme le montre la courbe ci dessous:
on obtiens
une solution plus précise comme le montre la courbe ci dessous:
![\includegraphics[width=0.5\textwidth]{CHAP1/uh3}](img73.png)
On peut aussi choisir comme fonctions de base des polynômes de degré
n. Par exemple, pour ![]() , les fonctions de base sont des polynômes
de degré 2 sur
, les fonctions de base sont des polynômes
de degré 2 sur ![]() , qui possèdent donc à priori 3 degrés de liberté.
Il faut de plus que ces fonctions vérifient les conditions aux limites
3.1, c.a.d s'annule en
, qui possèdent donc à priori 3 degrés de liberté.
Il faut de plus que ces fonctions vérifient les conditions aux limites
3.1, c.a.d s'annule en ![]() et
et ![]() , ce qui supprime
2 degrés de liberté. Dans ce cas il n'y a donc qu'une seule fonction
de base indépendante, que l'on choisit comme le polynôme de Lagrange
de degré 2, qui s'annule en
, ce qui supprime
2 degrés de liberté. Dans ce cas il n'y a donc qu'une seule fonction
de base indépendante, que l'on choisit comme le polynôme de Lagrange
de degré 2, qui s'annule en ![]() et
et ![]() , et qui vaut 1 en
, et qui vaut 1 en ![]() :
:
La solution ![]() s'écrit
s'écrit
où ![]() est solution de l'équation scalaire
est solution de l'équation scalaire
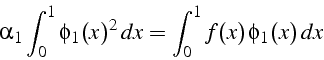
qui s'écrit en remplaçant ![]() par son expression et en calculant
les intégrales:
par son expression et en calculant
les intégrales:
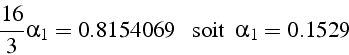
La solution obtenue est comparée à la solution exacte sur la figure ci dessous.
![\includegraphics[width=0.5\textwidth]{CHAP1/uhp2}](img83.png)
On remarque que le coefficient ![]() représente dans ce cas
la valeur nodale de
représente dans ce cas
la valeur nodale de ![]() en
en ![]() :
: