suivant: 4. Méthode des éléments monter: 3. Introduction aux éléments précédent: 3.2 Méthode des résidus Table des matières
La méthode des éléments finis est une méthode de construction d'une
approximation ![]() polynomiale par morceaux. Pour cela on découpe
le domaine de calcul en
polynomiale par morceaux. Pour cela on découpe
le domaine de calcul en ![]() éléments, et on choisit une interpolation
polynomiale de degré
éléments, et on choisit une interpolation
polynomiale de degré ![]() sur chaque élément. On construit les fonctions
de base par morceaux sur chaque élément comme des polynômes de degré
sur chaque élément. On construit les fonctions
de base par morceaux sur chaque élément comme des polynômes de degré
![]() .
.
Ainsi on découpe notre domaine ![]() en
en ![]() segments
segments
![]() , t.q.
, t.q.
![]() . Un exemple
de maillage est tracé sur la figure ci-dessous pour
. Un exemple
de maillage est tracé sur la figure ci-dessous pour ![]() .
.
![\includegraphics[width=0.5\textwidth]{CHAP1/mesh1D}](img92.png)
La solution approchée sur ce maillage est un polynôme de degré 2 sur
chacun des 2 éléments
![]() du maillage, qui est continue.
Cette solution possède donc 3 degrés de liberté par élément, correspondant
à 3 points d'interpolation: les 2 extrémités de l'élément et le noeud
milieu. Compte tenu de la continuité inter-élément et des conditions
aux limites 3.2, la solution approchée
du maillage, qui est continue.
Cette solution possède donc 3 degrés de liberté par élément, correspondant
à 3 points d'interpolation: les 2 extrémités de l'élément et le noeud
milieu. Compte tenu de la continuité inter-élément et des conditions
aux limites 3.2, la solution approchée ![]() possède au
total
possède au
total ![]() degrés de liberté. Ces degrés de liberté correspondent
à la valeur nodale de
degrés de liberté. Ces degrés de liberté correspondent
à la valeur nodale de ![]() aux noeuds internes
aux noeuds internes ![]() . Les 3
fonctions de bases associées sont appelées fonction de base
. Les 3
fonctions de bases associées sont appelées fonction de base ![]() :
ce sont les polynômes de Lagrange sur chaque élément, qui sont tracé
sur la figure ci-dessous:
:
ce sont les polynômes de Lagrange sur chaque élément, qui sont tracé
sur la figure ci-dessous:
![\includegraphics[width=0.6\textwidth]{CHAP1/bases}](img97.png)
La solution ![]() s'écrit donc sous la forme:
s'écrit donc sous la forme:
les valeurs inconnues étant les valeurs nodales
![]() aux noeuds internes.
aux noeuds internes.
Pour calculer ces valeurs nodales, on utilise la méthode des résidus
pondérés sous une forme faible. Partant de la relation 3.7,
on effectue une intégration par partie du terme en dérivée seconde,
ce qui donne, compte tenue des conditions aux limites vérifiées par
les fonctions tests ![]() :
:
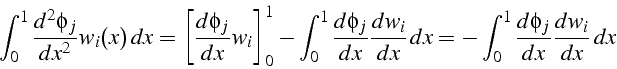
En reportant dans 3.7, on obtiens la formulation faible des résidus pondérés
Cette formulation faible est plus intéressante que la formulation
forte 3.7, car elle ne fait intervenir que des dérivées
premières, et donc la construction et le choix des fonctions de base
s'en trouve facilité. On peut ainsi choisir des fonction de base ![]() ,
i.e. polynomiales de degré 1 sur chaque élément. Cette formulation
faible a aussi une interprétation mécanique importante: elle correspond
à l'application du théorème des travaux virtuels (voir le cours
sur les éléments finis).
,
i.e. polynomiales de degré 1 sur chaque élément. Cette formulation
faible a aussi une interprétation mécanique importante: elle correspond
à l'application du théorème des travaux virtuels (voir le cours
sur les éléments finis).
En choisissant comme fonctions tests ![]() , les fonctions de base
, les fonctions de base
![]() associées au degré de liberté de
associées au degré de liberté de ![]() :
:
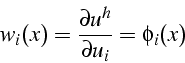
on obtiens le système linéaire ![]() permettant de calculer les valeurs
nodales
permettant de calculer les valeurs
nodales
![]()
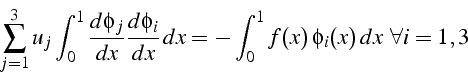
Après résolution, on a:
que l'on peut comparer avec les valeurs exactes en
![]()
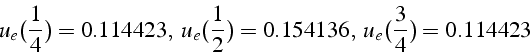
On constate que l'on a calculer la solution de
![]() avec une très bonne précision de 4 chiffres significatifs avec seulement
2 éléments.
avec une très bonne précision de 4 chiffres significatifs avec seulement
2 éléments.