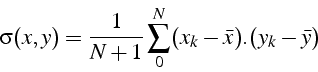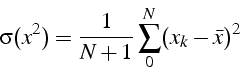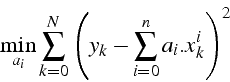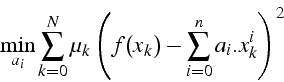7.2 Moindres carrés discrets

7.2.1 Cas général

Théorème:

soient N+1 points distincts ${x_{k}}$, alors il existe un polynôme unique p(x) de degré n ($n\le N$) $p(x)=\sum_{0}^{n}a_{i}.x^{i}$ réalisant la meilleure approximation de f(x) au sens de la norme euclidienne :

$$\min_{a_{i}}{\sum_{k=0}^{N}\left(f(x_{k})-\sum_{i=0}^{n}a_{i}.x_{k}^{i}\right)^{2}}$$

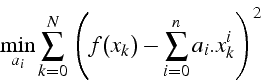
Ce polynôme p(x) est appelée l'approximation au sens des moindres carrés discrets de f .

7.2.1.1 Construction

Soient N+1 points distincts $x_{k}$, on veut déterminer les n+1 coefficients $a_{i}$ minimisant l'erreur :

$$E(a_{0},a_{1},\ldots a_{n})=\sum_{k=0}^{N}(f(x_{k})-\sum_{i=1}^{n}a_{i}.x_{k}^{i})^{2}$$

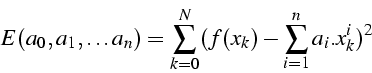
$E(a_{i})$ est une forme quadratique en $a_{i}$, et son minimum est atteint pour :

$$\frac{\partial E(a_{i})}{\partial a_{j}}=0\mbox{ pour j=0,n}$$

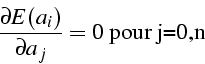
On obtient un système linéaire d'ordre n+1 :

$$A.x=B$$

avec $x=\{ a_{i}\}$, $A\in\mathbb{R}^{n+1}*\mathbb{R}^{n+1}$, $B\in\mathbb{R}^{n+1}$

7.2.2 Équation des moindres carrés

$$A=\left[\begin{array}{cccc} N+1 & \sum_{k=0}^{N}x_{k} & \ldo... ...{k}^{n+1} & \ldots & \sum_{k=0}^{N}x_{k}^{2n}\end{array}\right]$$

$$B=\left[\begin{array}{c} \sum_{k=0}^{N}y_{k}\\ \sum_{k=0}^{... ...{k}\\ \vdots\\ \sum_{k=0}^{N}x_{k}^{n}y_{k}\end{array}\right]$$

$$X=\left[\begin{array}{c} a_{0}\\ a_{1}\\ \vdots\\ a_{n}\end{array}\right]$$

Cette équation est ``l'équation normale''

$$A.X=B$$

7.2.3 Droite des moindres carrés

Approximation $p(x)=a_{0}+a_{1}.x$ $\leadsto$ ``équation normale''

$$A=\left[\begin{array}{cc} N+1 & \sum_{k=0}^{N}x_{k}\\ \sum_{k=0}^{N}x_{k} & \sum_{k=0}^{N}x_{k}^{2}\end{array}\right]$$

$$B=\left[\begin{array}{c} \sum_{k=0}^{N}y_{k}\\ \sum_{k=0}^{N}x_{k}y_{k}\end{array}\right]$$

$$X=\left[\begin{array}{c} a_{0}\\ a_{1}\end{array}\right]$$

en introduisant la moyenne des $x_{k}$ et $y_{k}$

$$\bar{x}=\frac{1}{N+1}\sum_{0}^{N}x_{k}\mbox{ et }\bar{y}=\frac{1}{N+1}\sum_{0}^{N}y_{k}$$

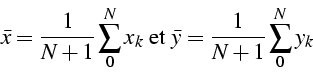
la covariance et la variance

$$\sigma(x,y)=\frac{1}{N+1}\sum_{0}^{N}(x_{k}-\bar{x}).(y_{k}-\bar{y})$$

$$\sigma(x^{2})=\frac{1}{N+1}\sum_{0}^{N}(x_{k}-\bar{x})^{2}$$

l'approximation $p(x)=a_{0}+a_{1}x$ par moindre carrés s'écrit alors:

$$a_{1}=\frac{\sigma(x,y)}{\sigma(x^{2})}$$

$$a_{0}=\bar{y}-a_{1}.\bar{x}$$

• le barycentre $(\bar{x},\bar{y})$ appartient à la droite des moindres carrés
• lissage des points expérimentaux $y_{k}$
  
  $$\min_{a_{i}}{\sum_{k=0}^{N}\left(y_{k}-\sum_{i=0}^{n}a_{i}.x_{k}^{i}\right)^{2}}$$
  
  

• poids de pondération $\mu_{k}$
  
  $$\min_{a_{i}}{\sum_{k=0}^{N}\mu_{k}\left(f(x_{k})-\sum_{i=0}^{n}a_{i}.x_{k}^{i}\right)^{2}}$$