7.1 Introduction

Soit f(x) une fonction sur [a,b], on cherche une approximation p(x) dans E (espace vectoriel) telle que: $\left\Vert f(x)-p(x)\right\Vert _{E}\mbox{minimum pour }p(x)\in E$

exemple:

approximation de $f(x)$ par $p(x)=a.x+b$

l'erreur $Err=\left\Vert f(x)-p(x)\right\Vert _{E}$ est fonction des 2 paramètres $(a,b)$

La condition de minimisation:

$$\begin{eqnarray*} \frac{\partial Err}{\partial a} & = & 0\\ \frac{\partial Err}{\partial b} & = & 0\end{eqnarray*}$$

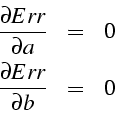
fournit 2 équations pour 2 inconnues.

Attention: la solution dépend du choix de la norme !!