suivant: 4.4 Conditionnement d'une matrice monter: 4. Résolution de système précédent: 4.2 Algorithme de GAUSS Table des matières
1ère version (boucle par colonnes)
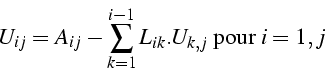
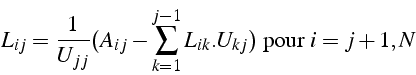
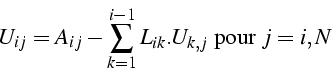
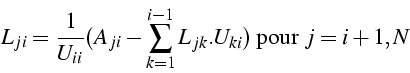
![]()
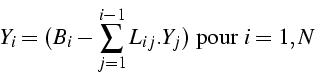
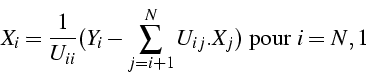
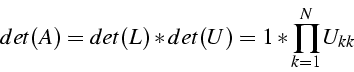
Calcul de ![]() par colonne par résolution de système linéaire
par colonne par résolution de système linéaire
Pour la colonne j : ![]() de
de ![]() on résout
on résout