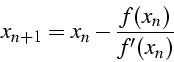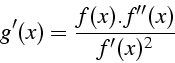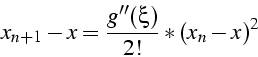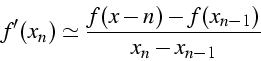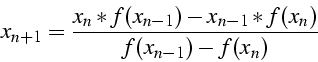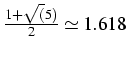Sous-sections
- théorème:
- Si f est 2 fois continûment dérivable au voisinage
de la racine
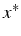 , et si
, et si
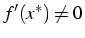 , alors il existe un
voisinage V de
, alors il existe un
voisinage V de 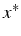 t.q.
t.q.
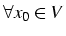 la méthode de Newton
converge vers
la méthode de Newton
converge vers 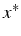 et est d'ordre 2.
et est d'ordre 2.
- demonstration
-
- méthode de la sécante
on construit l'intersection à partir des 2 derniers points
- meilleure convergence si fonction régulière
- variante: méthode Regula Falsi on choisit les 2 points qui encadrent
la racine
- méthode de la sécante d'ordre
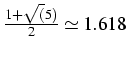
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2007-11-26