Sous-sections
englishrecherche des racines par point fixe (Newton)
- Point fixe:
- solutions de
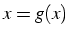
- Méthode du point fixe:
- A partir de
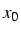 donné, construction
de la suite
donné, construction
de la suite 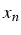 à l'aide de l'itération
à l'aide de l'itération
- Remarque:
- si la suite
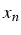 converge, elle converge vers un
point fixe de G(x)
converge, elle converge vers un
point fixe de G(x)
- théorème:
- Si g est différentiable au voisinage d'un point fixe
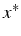 , et si
, et si
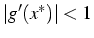 alors
alors 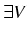 voisinage
de
voisinage
de 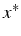 t.q.
t.q.
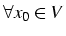 la suite
la suite
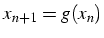 converge vers
converge vers 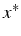
- démonstration:
- D.L de g(x) au voisinage de
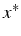
si
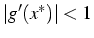 alors
alors
![$\exists V=[a,b]$](img108.png) t.q.
t.q.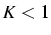 et
et ![$x_{0}\in[a,b]$](img110.png) d'où la convergence
d'où la convergence
- remarque:
- Dans la pratique, on choisit un intervalle
![$[a,b]$](img89.png) t.q.
t.q.
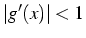 sur
sur ![$[a,b]$](img89.png) (car on ne connaît pas
(car on ne connaît pas 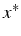 )
)
intersection de la droite 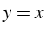 avec la courbe
avec la courbe 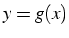
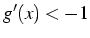 divergence
divergence
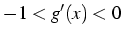 convergence alternée
convergence alternée
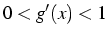 convergence monotone
convergence monotone
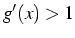 divergence
divergence
- Domaine
- d'attraction d'un point fixe: Points fixes attractifs
ou répulsifs
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2007-11-26
![]() avec la courbe
avec la courbe ![]()