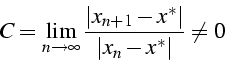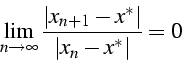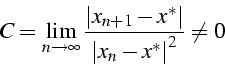- Suite d'ordre 1:
- soit
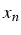 une suite convergeant vers
une suite convergeant vers 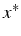 .
On dit que la suite
.
On dit que la suite 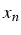 est d'ordre
est d'ordre 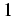 si:
si:
- vitesse
- de cvge=
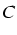
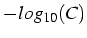 chiffres
exactes /iter.
chiffres
exactes /iter.
- Suite d'ordre 2:
- la suitep
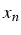 est d'ordre
est d'ordre 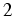 si:
si:
- vitesse
- de cvge=2
 double le nombre de chiffres
exactes /iter.
double le nombre de chiffres
exactes /iter.
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2007-11-26