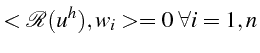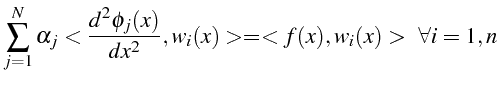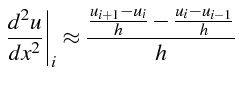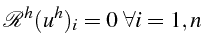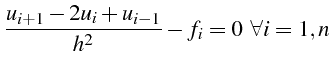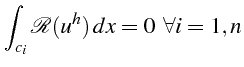On cherche une solution approchée 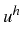 de (3). Cette
solution approchée
de (3). Cette
solution approchée 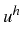 doit minimiser (au sens d'une certaine
norme) de résidu
doit minimiser (au sens d'une certaine
norme) de résidu
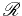 . Pour cela, il existe trois grandes
classes de méthodes:
. Pour cela, il existe trois grandes
classes de méthodes:
- la méthode des résidus pondérés (dont fait partie la méthode
des éléments finis):
on construit un espace d'approximation 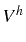 de dimension
de dimension 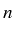 avec une base
avec une base
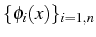 et on approxime la solution
et on approxime la solution
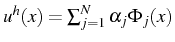 sur cette base. Les
inconnues
sur cette base. Les
inconnues
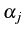 sont déterminer de telles sorte que la norme
du résidu soit minimum, i.e. que le résidu soit orthogonal à un espace
de fonctions tests
sont déterminer de telles sorte que la norme
du résidu soit minimum, i.e. que le résidu soit orthogonal à un espace
de fonctions tests 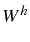 de base
de base
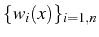 :
:
qui conduit au système linéaire:
En éléments finis, la méthode de Galerlin consiste à choisir
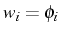
- la méthode des différences finies:
on discrétise l'équation sur un maillage équi-réparti
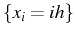 en approchant les opérateurs différentielles aux noeuds par des différences
en fonction des valeurs nodales
en approchant les opérateurs différentielles aux noeuds par des différences
en fonction des valeurs nodales 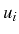 :
:
puis en imposant que le résidu discret associée
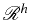 s'annule aux noeuds du maillage
s'annule aux noeuds du maillage
soit:
Il suffit ensuite de résoudre ce système linéaire tri-diagonal pour
déterminer les valeurs nodales 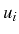 de la solution approchée
de la solution approchée 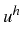
- la méthode des volumes finies
on discrétise le domaine 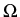 en volume élémentaire
en volume élémentaire 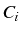 (cellule), et on écrit que la moyenne (intégrale) du résidu est nulle
sur chaque cellule
(cellule), et on écrit que la moyenne (intégrale) du résidu est nulle
sur chaque cellule
ce qui conduit à nouveau à un système linéaire sur la moyenne de 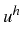 sur chaque cellule:
sur chaque cellule:
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2008-04-07
![]() de (3). Cette
solution approchée
de (3). Cette
solution approchée ![]() doit minimiser (au sens d'une certaine
norme) de résidu
doit minimiser (au sens d'une certaine
norme) de résidu
![]() . Pour cela, il existe trois grandes
classes de méthodes:
. Pour cela, il existe trois grandes
classes de méthodes: