suivant: 4.4 Chocs en tuyère monter: 4. Ondes de Choc précédent: 4.2 Relations à travers Table des matières
L'analyse précédente peut se généraliser au cas d'un choc droit se
déplaçant avec une vitesse constante ![]() dans un milieu au repos.
A l'amont du choc la vitesse est nulle, le fluide au repos, la masse
volumique vaut
dans un milieu au repos.
A l'amont du choc la vitesse est nulle, le fluide au repos, la masse
volumique vaut ![]() et la pression
et la pression ![]() , et à l'arrière
du choc la vitesse vaut
, et à l'arrière
du choc la vitesse vaut ![]() , la masse volumique
, la masse volumique ![]() ,
et la pression
,
et la pression ![]() .
.
Pour se ramener au cas du choc droit stationnaire, on considère un repère lié au choc. Dans ce repère l'écoulement amont est donné par:
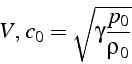
et l'écoulement aval par:
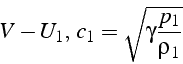
Les relations 4.54.64.9 sont toujours valables, mais en remplaçant :
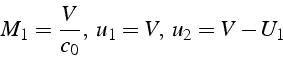
On considère un tube de longueur ![]() , séparé en son milieu par une
membrane avec d'un coté un gaz à haute pression (
, séparé en son milieu par une
membrane avec d'un coté un gaz à haute pression (
![]() )
et de l'autre un gaz à basse pression (
)
et de l'autre un gaz à basse pression (
![]() ).
).
![\includegraphics[width=0.6\textwidth]{CHAP4/dessin}](img672.png)
On enlève la membrane à l'instant ![]() . On introduit donc une discontinuité
de pression, masse volumique et température dans le tube.
. On introduit donc une discontinuité
de pression, masse volumique et température dans le tube.
Due à la différence de pression, le gaz de la chambre haute pression
va se déplacer dans la chambre basse pression. Une zone entre les
2 gaz se met en mouvement avec une vitesse ![]() et une pression
et une pression
![]() :
:
![]() avec en amont la propagation d'une
onde de choc avec une célérité
avec en amont la propagation d'une
onde de choc avec une célérité
![]() .
En arrière de cette zone se développe des ondes de détente de pente
.
En arrière de cette zone se développe des ondes de détente de pente
![]() :
:
![]() . Enfin, si on néglige la diffusion,
les deux gaz ne se mélangent pas, et la séparation entre les deux
correspond à une discontinuité de contact qui se propage avec la vitesse
. Enfin, si on néglige la diffusion,
les deux gaz ne se mélangent pas, et la séparation entre les deux
correspond à une discontinuité de contact qui se propage avec la vitesse
![]() .
.
On a donc le développement de 3 ondes dans le système:
Sur l'animation suivante, on a tracé l'évolution de la trajectoire des particules fluides dans un tube à choc, ainsi que l'évolution de la pression, de la vitesse, de la masse volumique et du nombre de Mach dans le tube en fonction du temps.
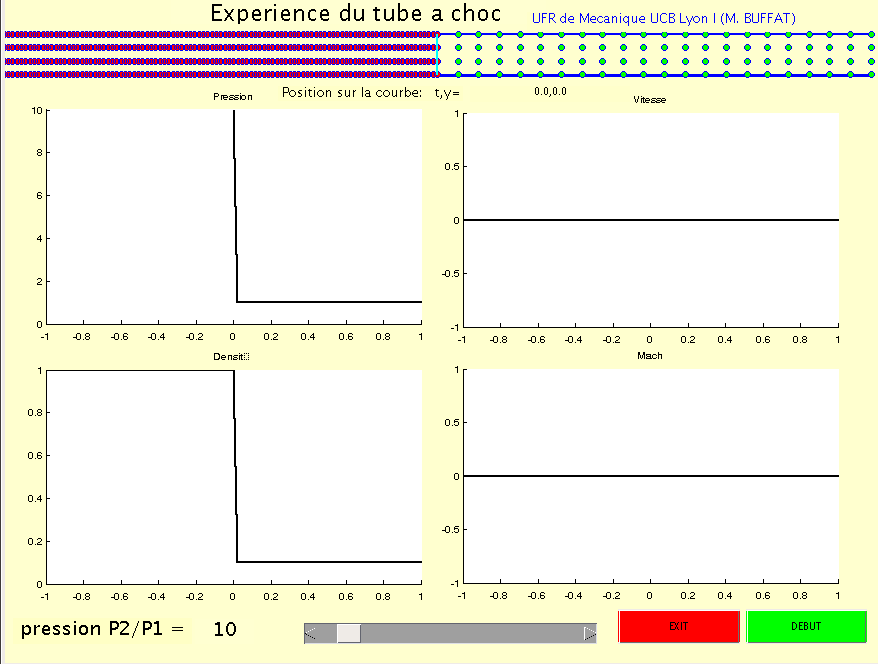
Cliquez ici pour voir l'animation
Dans l'expérience décrite au chapitre 3, on a créé un choc par déplacement d'un piston.
En utilisant les relations caractéristiques, dans la région entre
le piston (qui génère le choc) et le choc (i.e. à l'arrière du choc),
la célérité du son ![]() vérifie:
vérifie:
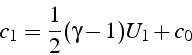
(puisque ![]() est la célérité dans le fluide au repos)
est la célérité dans le fluide au repos)
En utilisant cette relation dans l'équation de conservation de l'enthalpie totale à travers le choc 4.3:
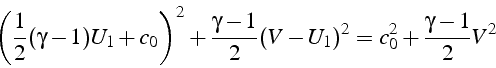
on en déduit la vitesse du choc
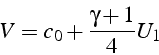
On note donc que par rapport au choc, l'écoulement amont est supersonique
![]() et l'écoulement aval est subsonique
et l'écoulement aval est subsonique
![]() .
.
On note aussi que la vitesse du choc ![]() est la moyenne de la vitesse
de propagation à l'amont et à l'aval du choc:
est la moyenne de la vitesse
de propagation à l'amont et à l'aval du choc:
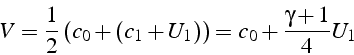
Sur l'animation suivante, on a tracé l'évolution de la trajectoire des particules fluides dans le piston.
Cliquez ici pour voir l'animation