suivant: 4.3 Choc instationnaire monter: 4. Ondes de Choc précédent: 4.1 Introduction Table des matières
Pour cela on considère un choc droit immobile à travers lequel l'écoulement reste quasi-unidimensionnel et stationnaire. Si le choc se déplace, on fait l'analyse dans un repère lié au choc.
On note ![]() ,
, ![]() ,
,
![]() l'état du fluide avant
le choc et
l'état du fluide avant
le choc et ![]() ,
, ![]() ,
,
![]() l'état du fluide
après le choc.
l'état du fluide
après le choc.
![\includegraphics[width=0.4\textwidth]{CHAP4/choc}](img618.png)
On fait des bilans (de masse, de quantité de mouvement et d'énergie)
en considérant un petit élément de volume ![]() incluant le choc. Ces
équations s'écrivent:
incluant le choc. Ces
équations s'écrivent:
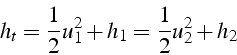
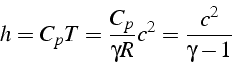
la dernière équation s'écrit:
Ce système d'équations est connue sous le nom de relations de Rankine-Hugoniot.
Nous allons calculer les variations des quantités à travers le choc
en fonction du nombre de Mach amont
![]()
En divisant par
![]() l'équation 4.2,
il vient:
l'équation 4.2,
il vient:
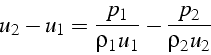
et en introduisant la célérité du son
![]() ,
il vient:
,
il vient:
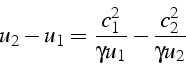
En utilisant l'équation 4.3, on calcule:
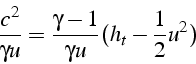
et on remplace:
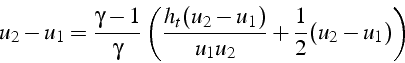
Or on a supposé qu'il y avait un choc et donc une discontinuité sur
la vitesse: i.e.
![]()
En simplifiant par ![]() , il vient:
, il vient:
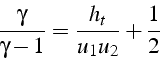
soit:
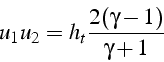
ce qui nous permet de calculer le rapport
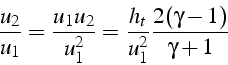
Et d'après 4.3, on a
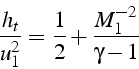
d'où l'expression de la variation de la vitesse à travers le choc:
On en déduit la variation de la masse volumique
La relation 4.3 permet de calculer la variation de célérité du son
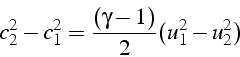
et en divisant par ![]() , on obtient la variation du Mach
, on obtient la variation du Mach
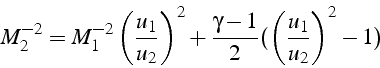
soit
Pour la pression, on utilise l'équation 4.2
d'où
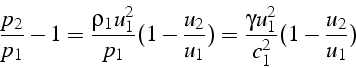
ce qui donne en remplaçant
![]()
Enfin en utilisant la définition de l'entropie (pour un gaz parfait):
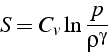
on obtient l'évolution de l'entropie à travers le choc:
On a tracé sur la figure ci-dessous l'évolution du saut d'entropie
4.9 en fonction du Mach amont ![]() ainsi que le rapport
le Mach
ainsi que le rapport
le Mach ![]() (relation sqrt(4.6)*M1)
(relation sqrt(4.6)*M1)
![\includegraphics[width=0.4\textwidth]{CHAP4/entropie}](img653.png)
![\includegraphics[width=0.4\textwidth]{CHAP4/machM2}](img654.png)
De cette analyse on déduit que:
![\includegraphics[width=0.5\textwidth]{CHAP4/chocdroit}](img661.png)
Comme nous l'avons vu précédemment, un choc droit permet de décélérer
l'écoulement:
![]() , à travers une compression forte
adiabatique
, à travers une compression forte
adiabatique ![]() et
et
![]() . L'énergie cinétique
de l'écoulement est transformée en énergie interne par augmentation
de l'agitation moléculaire: la température augmente à travers un choc
. L'énergie cinétique
de l'écoulement est transformée en énergie interne par augmentation
de l'agitation moléculaire: la température augmente à travers un choc
![]() .
.
On constate aussi que plus le Mach amont est fort, plus le choc est
fort, mais il y a une limite : le Mach aval ne peut descendre en dessous
d'une valeur limite
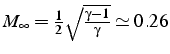 ,
ainsi que le saut de vitesse :
,
ainsi que le saut de vitesse :
![]() , et le saut de masse volumique
, et le saut de masse volumique
![]() .
Par contre le saut de pression n'est pas borné et tend vers l'infini.
.
Par contre le saut de pression n'est pas borné et tend vers l'infini.