4.1 Introduction

Nous avons vu dans les chapitres précédents que dans les écoulements compressibles peuvent apparaıtre des zones de discontinuité, par suite par exemple de concentration d'ondes se propageant à des vitesses différentes (caractéristiques). Les équations d'Euler permettent de décrire ces discontinuités (ou chocs).

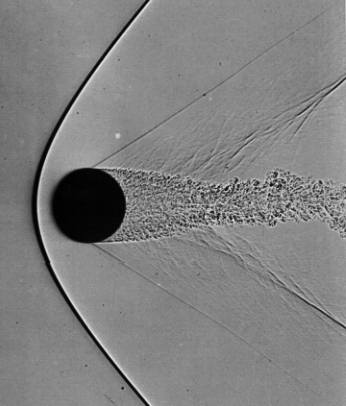
Dans la réalité, ces chocs apparaissent comme une très fine région de l'espace où l'on observe de très forte variation des propriétés thermodynamiques $T,\rho,p$ et de la vitesse $U$ du fluide. L'épaisseur d'un choc permet cependant de continuer à utiliser l'hypothèse de milieu continu.

Nous les modèliserons cependant comme des discontinuités mathématiques.

Dans un choc, il n'y a pas de création ni destruction de masse: donc l'équation de bilan de masse s'applique à travers le choc. De même, il n'y a pas de force extérieure qui s'applique dans un choc, donc on peut appliquer la bilan de quantité de mouvement. Finalement, il n'y a pas d'apport de chaleur extérieur, donc un choc est adiabatique (mais pas isentropique !).

A travers un choc, la température est discontinue. Donc un choc est une région où on transforme une partie de l'énergie cinétique (vitesse moyenne organisée des particules) en énergie interne (fluctuations internes désorganisées des particules: chaleur ou température). Et ceci ne peut se faire que dans un sens d'après le second principe: du mouvement organisé vers un mouvement désordonné. A travers un choc, l'écoulement est adiabatique, mais son entropie augmente: $dS>0$.