2.4 Bilan d'énergie

Pour un écoulement stationnaire et adiabatique d'un fluide parfait, l'équation de bilan locale de l'énergie totale s'écrit:

$$div((\rho e+\frac{1}{2}\rho U^{2}+p)\overrightarrow{U})=0$$

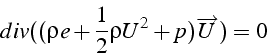
Le terme $e+\frac{1}{2}U^{2}=e_{t}$ représente l'énergie totale par unité de masse. Le terme $h=e+\frac{p}{\rho}$ correspond à l'enthalpie par unité de masse, et le terme $h+\frac{1}{2}U^{2}=e+\frac{p}{\rho}+\frac{1}{2}U^{2}=h_{t}$ l'enthalpie totale par unité de masse.

On en déduit que pour un écoulement stationnaire, le flux d'enthalpie totale est nul à travers n'importe quelle surface fermée S (théorème de la divergence)

$$\int_{S}\rho(h+\frac{1}{2}U^{2})\overrightarrow{U}.\overrightarrow{n}\, dS=0$$

De façon générale, si la surface de contrôle contient une section d'entrée $S_{1}$, une section de sortie $S_{2}$, l'équation s'écrit:

$$\int_{S_{1}}\rho_{1}(h_{1}+\frac{1}{2}U_{1}^{2})\overrightar... ...1}{2}U_{2}^{2})\overrightarrow{U_{2}}.\overrightarrow{n}\, dS=0$$

Le flux d'entalpie totale se conserve entre l'entrée et la sortie.

En considérant le cas du domaine de la figure 2.1, l'équation s'écrit:

$$-\rho_{1}(h_{1}+\frac{1}{2}U_{1}^{2})U_{1}S_{1}+\rho_{2}(h_{2}+\frac{1}{2}U_{2}^{2})U_{2}S_{2}=0$$